Wie viel Luft verbraucht (m)ein Motor?
Liebe Freunde,
Ich habe mir letzthin mal überlegt, wie viel Luft eigentlich ein Motor so verbraucht/verbrennt.
Dabei bin ich auf zwei Ansätze gestossen, die aber sehr unterschiedliche Werte ergeben.
Könnt ihr mir hier mal weiterhelfen und den Knopf in meinem Kopf lösen?
Also ganz konkrete Werte:
Motor: 4-Takt, 4-Zylinder mit 1261ccm
Fahrstrecke: 210km
Benzinverbrauch (laut Zapfsäule): 11.35 Liter
Mittlere Drehzahl: 2500U/min
Fahrzeit: 4 Stunden.
Nun habe ich einmal mit dem Verbrennungsluftverhältnis gerechnet:
1kg Benzin braucht bei Lambda=1 stöchiometrisch gerechnet 14.7kg Luft zur Verbrennung.
Benzin hat eine Dichte von 0.75kg/l, also sind die Verbrannten 11.35 Liter = 8.5125kg
Diese 8.5125kg haben also 125.13375 kg Luft benötigt, um verbrannt zu werden.
Luft hat eine Dichte von 1.224 kg/m3 bei 20°C (was es auch etwa war).
Die 125.13375kg Luft würden also 102.233m3 oder 102'233 Litern entsprechend.
Wenn ich aber mit dem Hubraum und der Drehzahl rechne:
4 Stunden = 240 Minuten * 2500 U/min = 600'000 U der Kurbelwelle.
Weil 4 Takt: Geteilt durch 2. Also 300'000 mal den Motor komplett geflutet.
300'000 x 1261ccm = 378'300 Liter.
Wäre es eine Abweichung von von mir aus 25% oder so würde ich sagen okay, was solls.
Aber hier geht es um den Faktor 3!
Das Benzin läuft ja nicht unverbrannt hinten aus dem Auspuff, also muss es vollständig verbrannt worden sein und die Menge Sauerstoff und somit die Menge Luft, die dazu nötig ist, kann man berechnen (eben 14.7kg Luft/kg Benzin). Und andererseits hat der Motor auch so oft gedreht, wie er halt gedreht hat und wurde auch so oft geflutet. Auch das lässt sich nicht wegdiskutieren.
Ich wäre froh, wenn mir jemand erklären könnte, warum es zu so einem grossen Unterschied in den beiden Rechnungen kommt, resp. wie es denn richtig wäre.
Vielen Dank und Gruss
Christoph
Beste Antwort im Thema
Quatsch, ist doch ganz einfach: Deine Überlegung mit dem Hubraum basiert auf der Annahme, dass die Zylinder jeweils komplett mit Luft bei Umgebungsdruck (also ohne Aufladung) gefüllt werden. Das würde aber bedeuten, dass der Motor permanent auf Volllast laufen würde (Drosselklappe komplett geöffnet). Das wird bei einer Durchschnittsgeschwindigkeit von 52,5 km/h sicherlich nicht der Fall sein.
61 Antworten
Zitat:
Wäre zu einfach auf den Luftmengenmesser zu gucken wieviel g/s durchgehen. Quasi "unsportlich".
Ein Luftmengenmesser liefert Volumen/Sekunde.
Ein Luftmassenmesser liefert Gramm/Sekunde.
Das wäre wie Zeit messen mit der Stoppuhr. :-)
Halt: er müsste den (variablen) Luftmassenmesserwert (Gramm Luft pro Sekunde) noch über die Zeit integrieren, um auf eine Luftmasse zu kommen. Und diese Luftmasse müsste er dann - unter Annahme einer einer bestimmten Lufttemperatur und Höhe über NN und damit Luftdichte - in ein Luftvolumen umrechnen.
Luftmengenmesser? Die sind eigentlich schon länger nicht mehr üblich :-) Aber damit wärs dann wenigstens wieder etwas ungenauer- passend zum gesamten Ansatz.
Könnte er nicht auch über die Stömungsgeschwindigkeit durch eine Verengung und den dort herrschenden Druck auf die Menge und somit Masse koppeln? Temperaturkompensation natürlich integriert.
Zitat:
Falls es dich aber interessiert: Die Leistung bei 2500 rpm ist 32 hp net. nach SAE.
@rchr
Dankeschön, wenn der Motor soweit richtig abgestimmt ist dann sind es ca 26,6Gramm/Sek Luftmasse.
Ähnliche Themen
Zitat:
@Grasoman schrieb am 12. April 2020 um 19:25:08 Uhr:
Zitat:
Wäre zu einfach auf den Luftmengenmesser zu gucken wieviel g/s durchgehen. Quasi "unsportlich".
Ein Luftmengenmesser liefert Volumen/Sekunde.
Ein Luftmassenmesser liefert Gramm/Sekunde.Das wäre wie Zeit messen mit der Stoppuhr. :-)
Halt: er müsste den (variablen) Luftmassenmesserwert (Gramm Luft pro Sekunde) noch über die Zeit integrieren, um auf eine Luftmasse zu kommen. Und diese Luftmasse müsste er dann - unter Annahme einer einer bestimmten Lufttemperatur und Höhe über NN und damit Luftdichte - in ein Luftvolumen umrechnen.
Das ist ein danke wert.
Auch wenn die eigentliche Frage ja nicht dem Messen und rechnen, sondern nur dem rechnen gilt.
Auf das umrechnen in Volumen kann man auch verzichten.
Das hat der Themenstarter ja schon selbst gemacht.
Zitat:
Diese 8.5125kg haben also 125.13375 kg Luft benötigt, um verbrannt zu werden.
Luft hat eine Dichte von 1.224 kg/m3 bei 20°C (was es auch etwa war).
Die 125.13375kg Luft würden also 102.233m3 oder 102'233 Litern entsprechend.
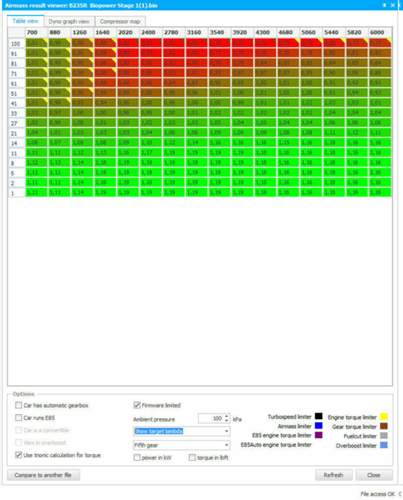
Also, wenn ich mal in mein Kennfeld vom Saab schaue.
Ich hoffe ich habe keinen bösen Denkfehler!
Bei 110km/h habe ich laut Bordcomputer Luftmasse-Soll-Wert von gemittelt etwa 255mg/c
Die Drehzahl liegt bei etwa 2400u/min
mg/c steht für Milligramm pro Combustion
Ungefähr 1224g Luft pro Minute oder 73,44kg Luft pro Stunde.
Bei genau den beiden Daten habe ich einen Punkt im Kennfeld im Airmass-Result-Viewer.
AFR liegt in dem Bereich laut Kennfeld bei 15,2 und Lambda bei 1,04
Fuelflow bei 6l/h (Nachkommastelle wird in der Übersicht gekürzt)
Da man in der Praxis nie perfekt gleichmäßige Bedingungen hat würde ich da noch ein paar Prozent draufrechnen.
Ich habe mal ein paar Screenshots der Übersicht angehangen, da kann man sich dann ein paar Punkte raussuchen.
Ich stelle euch mal Luftmasse in mg/c zur Verfügung, sowie Leistung, Lambda, AFR und Fuel Flow (l/h)
X-Achse ist Drehzahl und Y-Achse in diesem Fall das Pedalkennfeld.
Die Software entspricht nicht ganz der Serie da ich sie selbst geschrieben habe.
Die Abweichungen zur Seriensoftware befinden sich aber erst im Bereich über 700mg/c Luftmasse.
Die Kennfelder zeigen dies auf Basis der Benzinkennfelder.
Auf Basis der E85-Kennfelder könnte ich es bei Interesse nochmal gesondert einstellen.
Zitat:
@Anarchie-99 schrieb am 13. April 2020 um 17:42:39 Uhr:
Zitat:
Falls es dich aber interessiert: Die Leistung bei 2500 rpm ist 32 hp net. nach SAE.
@rchr
Dankeschön, wenn der Motor soweit richtig abgestimmt ist dann sind es ca 26,6Gramm/Sek Luftmasse.
Und das ist genau wieder der Vollast-Verbrauch, den wir auch mit der Rechnung nach Hubraum bekommen 😁
Aber das ist ja nicht verwunderlich, da die Leistung ja auf dem Prüfstand gemessen wurde und dort wird ja mit Volllast gefahren. Es zeigt einfach, dass die Rechnung stimmt 😁
Gehe ich richtig in der Annahme, dass du einfach die PS in kW umgerechnet, mit rpm die Zeit korrigiert und dann mit dem Brennwert von Benzin den Luftverbrauch errechnet hast?
Oder hast du noch eine andere Formel? Nur so für mein Interesse und meine Neugierde ;-)
@Leon596:
Das passt doch!
Also wenn du einen 4-Zylinder-Motor hast, dann komme ich auf die gleichen Werte.
2400 rpm x 4 Zylinder : 2 r/c = 4800 c/min x 0.255 g/c = 1224 g/min
6 l/h --> 4.5 kg/h x 14.7 kg/kg = 66.15 kg/h Luft = 1103 g/min
Die 10% Differenz würde ich mal auf das Weglassen der Nachkommastelle in deinem Verbrauch und halt dem Unterschied zwischen theoretischer Rechnung und Realität schieben...
Gruss
Christoph
Zitat:
@rchr schrieb am 14. April 2020 um 17:57:11 Uhr:
Zitat:
@Anarchie-99 schrieb am 13. April 2020 um 17:42:39 Uhr:
@rchr
Dankeschön, wenn der Motor soweit richtig abgestimmt ist dann sind es ca 26,6Gramm/Sek Luftmasse.Und das ist genau wieder der VollastVerbrauch, den wir auch mit der Rechnung nach Hubraum bekommen 😁
Aber das ist ja nicht verwunderlich, da die Leistung ja auf dem Prüfstand gemessen wurde und dort wird ja mit Volllast gefahren. Es zeigt einfach, dass die Rechnung stimmt 😁Gehe ich richtig in der Annahme, dass du einfach die PS in kW umgerechnet, mit rpm die Zeit korrigiert und dann mit dem Brennwert von Benzin den Luftverbrauch errechnet hast?
Oder hast du noch eine andere Formel? Nur so für mein Interesse und meine Neugierde ;-)Gruss
Christoph
Er hatte ja 2 Lösungsansätze.
1. Hier ging er wohl vom Bordcomputer aus.
Verbrauch n-Liter und davon den Luftverbrauch bei Lambda = 1 berechnet.
2 Drehzahl.
Hier war das Problem mit Volllast und Teillast und was ist sozusagen das wirksame Volumen.
Bzw der Druck im Zylinder bevor die Kompression einsetzt.
Zitat:
@Alexander67 schrieb am 14. April 2020 um 18:16:53 Uhr:
Er hatte ja 2 Lösungsansätze.
1. Hier ging er wohl vom Bordcomputer aus.
Verbrauch n-Liter und davon den Luftverbrauch bei Lambda = 1 berechnet.2 Drehzahl.
Hier war das Problem mit Volllast und Teillast und was ist sozusagen das wirksame Volumen.
Bzw der Druck im Zylinder bevor die Kompression einsetzt.
Ich denke, mit "Er" meinst du mich?
Ich bin nicht vom Bordcomputer ausgegangen, sondern vom effektiven Verbrauch an der Zapfsäule.
Laut Anarchie-99 gibt es aber wohl noch einen Weg über die Leistung. Hier habe ich gefragt, ob er die Leistung einfach in Benzin-Brennwert umgerechnet und so wieder auf den Verbrauch gekommen ist, oder ob er noch einen anderen Weg weiss.
Gruss
Christoph
Zitat:
@rchr schrieb am 14. April 2020 um 18:27:10 Uhr:
....
Laut Anarchie-99 gibt es aber wohl noch einen Weg über die Leistung. Hier habe ich gefragt, ob er die Leistung einfach in Benzin-Brennwert umgerechnet und so wieder auf den Verbrauch gekommen ist, oder ob er noch einen anderen Weg weiss.Gruss
Christoph
Ja gibt es.
Konnte ich vor 30 Jahren.
Die triviale Möglichkeit ist natürlich die über die Leistung und einen Wirkungsgrad den Verbrauch und dann weiter wie beim n-Liter Verbrauch. Das meine ich aber nicht.
Es gibt Standard - Prozesse in der Thermodynamik.
Und anhand von denen kann da auch einiges berechnen.
Ich denke ich hatte aber nie wirklich viel von diesen Berechnungen gehalten.
Zu viele Annahmen die ohne viele Erfahrungswerte nicht wert sind.
Aber nochmal, das ist 30 Jahre her. Eher noch mehr.
Eine (mechanische) Momentan-Leistung wie akuelle mechanische PS oder akuelle mechanische kW "einfach" in einen "Benzin-Brennwert" (also dann eine Art Energiemenge pro Zeit und dann Kraftstoffmasse oder Kraftstoffvolumen pro Zeit) umzurechnen ist schwierig, weil dazwischen der mechanische Motorwirkungsgrad ist, und der ist wiederum variabel.
Denn mal werden 10% des Heizwertes des verbrannten Kraftstoffes zu Vortrieb, und mal auch so 35% des Heizwertes des verbrannten Kraftstoffes.
Man braucht dafür das Muscheldiagramm=Verbrauchskennfeld des Motors - das gibt für eine Drehzahl die Gramm Kraftstoff pro kWh (mechanische Energie) zurück und damit kann man dann weiterrechnen.
https://de.wikipedia.org/wiki/Verbrauchskennfeld
Da das Ding aber höchst unlinear ist, rechnet es sich damit äußerst schlecht im Kopf. :-)
Und deswegen macht es viel Sinn, im unteren Lastbereich und dem üblichen "Lambda gleich 1" den Luftmassenstrom eines Betriebszustands zu nehmen und mit "Lambda" auf einen Brennstoffdurchsatz umzurechnen. Daraus kannste theoretisch auch auf alltagsrelevante Teile des Verbrauchskennfelds (Verbrauch sowie Wirkungsgrad bei konstant X km/h) zurückrechnen.