Turbobenziner: Abhängigkeit des Verbrauchs von Fahrweise

[nabenschalter]

Die Meinung ist weit verbreitet, dass Downsizing-Benziner ihre auf dem Papier niedrigen Verbrauchswerte nur bei angepasster Fahrweise einhalten. Zum Beispiel heißt es in einem Autotest vom ADAC (Peugeot 508 1.6 PureTech 180 Allure EAT8): „Insgesamt gesehen ist der Verbrauch heutzutage recht hoch, er hängt aber wie so oft bei Turbobenzinern stark von der Fahrweise ab“.

Ich fahre einen Berlingo (3. Generation) mit dem kleineren 1.2 PureTech Motor und der gleichen Wandlerautomatik und mache mir einen Sport daraus, möglichst sparsam zu fahren.

Zu dem 1.2 PureTech Motor liefert PSA ein Diagramm welches zeigt, dass der geringste Verbrauch CO2-Emissionen von 237 g/kWh entspricht. Dieser optimale Punkt liegt bei 2700 1/min und mittlerem Druck. PSA gibt aber auch an, dass der Bereich mit geringem Verbrauch (<= 240 g/kWh) sehr groß ist und sich bei mittleren Drücken von 1250 bis 4500 1/min erstreckt. Das Diagramm findet sich z.B. auf Seite 43 folgender Präsentation https://www.arts-et-metiers.asso.fr/.../840_compte_rendu.pdf

Nun zu meiner Frage: sollte beim 1.2 PureTech, einem typischen modernen Turbobenziner, der Verbrauch angesichts des Diagramms nicht gerade besonders *unabhängig* von der Fahrweise sein, zumindest weniger abhängig als bei anderen Motoren? Also gerade das Gegenteil der oben zitierten Behauptung? Oder spielen andere Faktoren eine Rolle? Welche?

Mir ist die Problematik des höheren Verbrauchs durch Volllastanreicherung bekannt. Aber kommt man bei einigermaßen gemäßigter Fahrweise überhaupt in diesen Bereich? Zumal beim 1.2 PureTech Vorkehrungen getroffen worden sind um die Volllastanreicherung zu vermeiden.

[GaryK]

Da ist zu viel Leistung im Spiel. Bzw. Drehmoment....

[Diabolomk]

Je nach dem was man will, fest gegen die Wand oder schnell 😉

Aber bleiben wir dabei, will ich das Auto schnell überholen lassen bzw. bin auf einer Auffahrt, neben mir ein LKW und die Beschleunigungsspur endet an einem Brückenpfeiler habe ich 3 Möglichkeiten.
Bremsen und hinter den LKW, auf der Drehmomentwelle beschleunigen oder nach Leistung gehen.
Die schlechteste Alternative ist die Drehmomentwelle!

[FWebe]

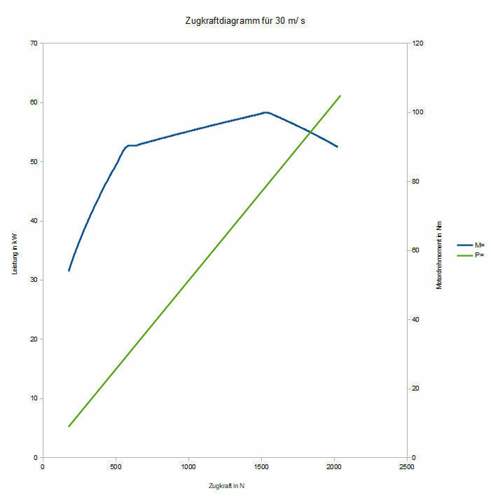
Dazu kann man sich mal die angehängte Grafik ansehen, wenn einem ein konventionelles Zugkraftdiagramm zu schwierig ist.

[TaifunMch]

Ich würde 'nen Panzer nehmen, ohne Turbo und die Brückenpfeiler wegballern.

[GaryK]

Geht nicht, APDFS oder HE bzw. HEAT machen Brückenpfeilern nicht wirklich was. Im Leo gehts wie bei Hardcore-LKW Fahrern - Blinker setzen und rüberziehen. Egal was da ist, das wird aus reinem Selbsterhaltungstrieb dir den Platz freimachen....

Ok, zurück zum Thema bitte.

[Diabolomk]

Bleiben wir dabei, sparsam lieber weniger Drehmoment als möglich, schneller auch 😉
Und doch mag ich Motoren mit viel Drehmoment durch kleine Turbos
Denn der Alltag findet in der Mitte statt und nicht bei Motoren mit wenig Drehmoment und Leistung irgendwie über Drehzahl, das ist dann doch irgendwie Kleinwagenfeeling.

Aber Apropos Platz freimachen, wenn das mal so einfach wäre.
Schonmal nen langen Iveco 3,5T mit Zwillingsreifen bei 120km/h hinten wegrutschen sehen? Ich danke dem LKW Fahrer heute noch, dass ich das Händeln durfte. Vollbremse ohne ABS bei leichter Beladung ist kein Spaß. Der Autofahrer links neben mir war beim ersten linksschlenk zum Glück schon weit genug vorne!

Aber anscheinend war es wichtig mit ~4km/h Differenzgeschwindigkeit zu überholen. Der hat wohl auch nur über Drehmoment geschaltet... 😉

[Timmerings Jan]

Zitat:

@Duke711 schrieb am 23. Juli 2020 um 00:55:05 Uhr:

Zitat:

@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:

Weit daneben. Du verwechselt "mal Null" mit "durch Null".

Aber sicher kommt hier noch ein Lösungsvorschlag wie man die o.g. Gleichung lösen kann, die ist übrigens so richtig.

Da war keine Gleichung zum Lösen, sondern nur noch eine Zahl zum berechnen. Und dein Ergebnis "Null" war nun mal weit daneben. Kannst du das akzeptieren?

Zitat:

Mit Doppelbrüchen scheinst Du wohl so deine Schwierigkeiten zu haben?

Deine Kompetenz, mit solchen Vorwürfen um dich zu werfen, muss ich gerade doch etwas anzweifeln.

Zitat:

Du verräst uns sicher wie Du mit a = P / (v * m) eine Beschleunigung aus dem Stand ermittelst.

Auf die gleiche Weise, wie du es in deiner komplizierteren Version der selben Gleichung bei rpm = 0 tust. Die hat dann nämlich das exakt gleiche Problem.

Auf den ersten Ansatz kommt dann in beiden Formen als Beschleunigung "unendlich" heraus, und im Rahmen der üblichen Gültigkeits-Grenzen physikalischer Grundlagen-Formeln in der komplizierten Wirklich stimmt das in gewissen Sinne sogar. Wenn es nämlich tatsächlich möglich wäre, im Stand eine Leistung größer als Null auf die Straße zu bringen, wäre das Ergebnis kein Anfahren, sondern ein knallharter Stoß, der sich dann mathematisch als scheinbar unendliche Beschleunigung darstellt.

Etwas praktischer gesprochen ist der Moment des Anfahrens beim Auto in aller Regel vollständig haftreibungs-limitiert; es spielen also weder Drehmoment noch Leistung des Motors irgendeine nennenswerte Rolle. Es kommt allein auf die maximal verfügbare Reibung der Reifen an. Der komplette Rest verdampft in der Kupplung, oder wird für Reifenquietschen aufgewendet.

Zitat:

Ebenso verräst Du uns mit a = P / (v * m) wie Du hier den Beschleunigunsverlauf innerhalb einer einzelnen Übersetzung genau auflösen kannst.

Indem man die tatsächliche Abhängigkeit der netto nutzbaren Leistung P(v) einsetzt, und durchrechnet. Das ist am Ende exakt die selbe Rechnung, die man auch mit dem Drehmomentverlauf M(v) oder mit der ebenfalls geschwindigkeitsabhängigen Radzugkraft F(v) machen würde.

[Rael_Imperial]

Zitat:

@Duke711 schrieb am 23. Juli 2020 um 00:55:05 Uhr:

Problem 1.
Bechleunigung aus dem Stand:a = (200000 / 0) / 1600 = 0

Zitat:

@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:

Weit daneben. Du verwechselt "mal Null" mit "durch Null".

Ich glaube Du verwechselst hier was. Aber sicher kommt hier noch ein Lösungsvorschlag wie man die o.g. Gleichung lösen kann, die ist übrigens so richtig. Mit Doppelbrüchen scheinst Du wohl so deine Schwierigkeiten zu haben?

Der Punkt geht an Timmerings Jan: Der erste Bruch lautet a = (200000 / 0). Und das geht gegen Unendlich. Der zweite Bruch / 1600 tut da nichts mehr zur Sache. Die

theoretische

Beschleunigung bei v = 0 ist also Unendlich, nicht Null.

Zitat:

@Duke711 schrieb am 23. Juli 2020 um 00:55:05 Uhr:

Zitat:

@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:

Und wenn dir jetzt noch klar wird, dass (2 * pi * r * rpm * I * 60) nichts anderes als eine komplizierte Schreibweise für die Geschwindigkeit ist, steht da:

a = P / (v * m)

Was, oh Wunder, genau die Gleichung ist, die so vehement ablehnst.

Ich bitte doch etws mehr um Respekt, wenn Du schon einen Sachverhalt als falsch deklarierst, sollte Du dich wengisten noch um eine sachliche Begründung bemühen.
Du verräst uns sicher wie Du mit a = P / (v * m) eine Beschleunigung aus dem Stand ermittelst. Solange hier keine sachlichen Argumente folgen stufe ich deinen Kommentar als unseriös ohne nenneswerten Inhalt ein. Ebenso verräst Du uns mit a = P / (v * m) wie Du hier den Beschleunigunsverlauf innerhalb einer einzelnen Übersetzung genau auflösen kannst.

Auch ein Punkt für Timmerings Jan (abgesehen von der Tatsache, dass die Formel korrekt lautet:

(2 * pi * r * rpm

/

I * 60).

Und jetzt mal zum Wesentlichen:
Die beiden Fraktionen "Leistung" und "Drehmoment" stehen sich hier derart verbissen gegenüber, dass sie gar nicht mehr merken, dass beide Recht haben und lediglich dieselben physikalischen Zusammenhänge aus zwei verschiedenen Blickwinkeln betrachten.

In meiner beruflichen Tätigkeit habe ich ebenfalls schon nette Modelle zur Berechnung der Fahrzeugbewegung erstellt. Dabei habe ich tatsächlich, dem alten Newton folgend, ebenfalls den naheliegenden Weg über die Kraft respektive Drehmoment genommen. Letztlich wird ein Fahrzeug durch das Überschussmoment, welches am Rad anliegt, beschleunigt. Also das Moment, welches nach Abzug der zu überwindenden Roll- und Luftwiderstandsmomente übrig bleibt. Zur Vereinfachung lasse ich diese im Folgenden weg, betrachte also nur niedrige Geschwindigkeiten.

Dann ist die momentane Beschleunigung in einem festen Gang tatsächlich proportional zum Raddrehmoment und über die Getriebeübersetzung somit zum Motordrehmoment. Das erklärt einleuchtend, weshalb in höheren Gängen die Beschleunigung niedriger ausfällt.

So, nachdem ich jetzt der Momentenfraktion Recht gegeben habe, kommt nun die Leistungsfraktion dran:
Wann erreiche ich bei einer bestimmten Geschwindigkeit die höchste Beschleunigung? Nun, wie wir oben festgestellt haben dann, wenn das Radmoment am größten ist. Mit einer bestimmten Geschwindigkeit ist aber untrennbar eine bestimmte Raddrehzahl verbunden. mit dieser und dem Raddrehmoment lässt sich leicht die Radleistung ausrechnen. Also folgt ganz logisch, dass zur Erzielung einer hohen Beschleunigung die Radleistung möglichst hoch sein muss. Und das erreicht man, indem man die Getriebeübersetzung (Gang) so wählt, dass der Motor möglichst in seinem Leistungsmaximum betrieben wird.

Die Höchstgeschwindigkeit erreicht man dann, wenn das Gleichgewicht aus Fahrwiderständen und Antriebsleistung auf den Punkt der Motorhöchstleistung fällt.

Beide Fraktionen vergessen hier häufig den Einfluss des Getriebes, betrachten nur den Motor und diskutieren ständig aneinander vorbei. Dann kommt so etwas dabei heraus:

"Hmm sehr komisch, trotz der gleichen Leistung ist im 1. Gang die Beschleunigung größer als im 5. Gang. Wie kann das sein, es soll ja angeblich die Leistung das Fahrzeug beschleunigen?"

Bedenkt meine obigen Ausführungen und begrabt das Kriegsbeil.
Wie gesagt, ihr redet über das Gleiche, nur aus zwei unterschiedlichen Blickwinkeln. Der Physik dahinter ist das aber völlig egal. Sie ändert sich dadurch nicht.

[TaifunMch]

Zitat:

@Rael_Imperial schrieb am 23. Juli 2020 um 22:44:29 Uhr:

Zitat:

@Duke711 schrieb am 23. Juli 2020 um 00:55:05 Uhr:

Problem 1.
Bechleunigung aus dem Stand:

a = (200000 / 0) / 1600 = 0

Ich glaube Du verwechselst hier was. Aber sicher kommt hier noch ein Lösungsvorschlag wie man die o.g. Gleichung lösen kann, die ist übrigens so richtig. Mit Doppelbrüchen scheinst Du wohl so deine Schwierigkeiten zu haben?

Der Punkt geht an Timmerings Jan: Der erste Bruch lautet a = (200000 / 0). Und das geht gegen Unendlich.

Da dreht sich mir als Mathematiker der Magen um. Das geht nicht gegen unendlich, sondern das ist ganz einfach undefiniert.

"Die ist übrigens so richtig" ... loool. Da ist nix richtig und auch das = 0 ist Blödsinn.

[Rael_Imperial]

Für den Mathematiker hast Du sicherlich Recht, ich bin aber Ingenieur. Und für den läuft lim(p/v) für v -> 0 gegen Unendlich.

[TaifunMch]

Wenn ihr wollt, dass euch noch irgendwer folgt, dann solltet ihr vielleicht schreiben, welcher Wert da nahezu 0 sein soll.

Wobei die meisten hier nur noch am lachen sind. So wie ihr hier diskutiert würdet ihr im Reallife nie miteinander umgehen.

[Rael_Imperial]

Zitat:

@TaifunMch schrieb am 23. Juli 2020 um 23:06:09 Uhr:

Wenn ihr wollt, dass euch noch irgendwer folgt, dann solltet ihr vielleicht schreiben, welcher Wert da nahezu 0 sein soll.

Steht doch da oben: v.

Falls Du die Bedeutung von v nicht kennen solltest: Geschwindigkeit.

[Go}][{esZorN]

Zitat:

@TaifunMch schrieb am 23. Juli 2020 um 23:6:09 Uhr:

Wobei die meisten hier nur noch am lachen sind. So wie ihr hier diskutiert würdet ihr im Reallife nie miteinander umgehen.

Den ersten Satz würde ich so nicht unterschreiben, zum zweiten denke ich, dass es hier allmählich gesitteter zugeht.

Es war aber in der letzten Zeit ziemlich respektlos, da gebe ich dir recht.

[Rael_Imperial]

Deshalb habe ich versucht, eine Brücke zwischen beiden Fraktionen zu bauen.

[Go}][{esZorN]

Finde ich auch gut. 🙂