Turbobenziner: Abhängigkeit des Verbrauchs von Fahrweise
Die Meinung ist weit verbreitet, dass Downsizing-Benziner ihre auf dem Papier niedrigen Verbrauchswerte nur bei angepasster Fahrweise einhalten. Zum Beispiel heißt es in einem Autotest vom ADAC (Peugeot 508 1.6 PureTech 180 Allure EAT8): „Insgesamt gesehen ist der Verbrauch heutzutage recht hoch, er hängt aber wie so oft bei Turbobenzinern stark von der Fahrweise ab“.
Ich fahre einen Berlingo (3. Generation) mit dem kleineren 1.2 PureTech Motor und der gleichen Wandlerautomatik und mache mir einen Sport daraus, möglichst sparsam zu fahren.
Zu dem 1.2 PureTech Motor liefert PSA ein Diagramm welches zeigt, dass der geringste Verbrauch CO2-Emissionen von 237 g/kWh entspricht. Dieser optimale Punkt liegt bei 2700 1/min und mittlerem Druck. PSA gibt aber auch an, dass der Bereich mit geringem Verbrauch (<= 240 g/kWh) sehr groß ist und sich bei mittleren Drücken von 1250 bis 4500 1/min erstreckt. Das Diagramm findet sich z.B. auf Seite 43 folgender Präsentation https://www.arts-et-metiers.asso.fr/.../840_compte_rendu.pdf
Nun zu meiner Frage: sollte beim 1.2 PureTech, einem typischen modernen Turbobenziner, der Verbrauch angesichts des Diagramms nicht gerade besonders *unabhängig* von der Fahrweise sein, zumindest weniger abhängig als bei anderen Motoren? Also gerade das Gegenteil der oben zitierten Behauptung? Oder spielen andere Faktoren eine Rolle? Welche?
Mir ist die Problematik des höheren Verbrauchs durch Volllastanreicherung bekannt. Aber kommt man bei einigermaßen gemäßigter Fahrweise überhaupt in diesen Bereich? Zumal beim 1.2 PureTech Vorkehrungen getroffen worden sind um die Volllastanreicherung zu vermeiden.
Beste Antwort im Thema
Zitat:
@Duke711 schrieb am 23. Juli 2020 um 00:55:05 Uhr:
Problem 1.
Bechleunigung aus dem Stand:a = (200000 / 0) / 1600 = 0
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Weit daneben. Du verwechselt "mal Null" mit "durch Null".
Ich glaube Du verwechselst hier was. Aber sicher kommt hier noch ein Lösungsvorschlag wie man die o.g. Gleichung lösen kann, die ist übrigens so richtig. Mit Doppelbrüchen scheinst Du wohl so deine Schwierigkeiten zu haben?
Der Punkt geht an Timmerings Jan: Der erste Bruch lautet a = (200000 / 0). Und das geht gegen Unendlich. Der zweite Bruch / 1600 tut da nichts mehr zur Sache. Die
theoretischeBeschleunigung bei v = 0 ist also Unendlich, nicht Null.
Zitat:
@Duke711 schrieb am 23. Juli 2020 um 00:55:05 Uhr:
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Und wenn dir jetzt noch klar wird, dass (2 * pi * r * rpm * I * 60) nichts anderes als eine komplizierte Schreibweise für die Geschwindigkeit ist, steht da:a = P / (v * m)
Was, oh Wunder, genau die Gleichung ist, die so vehement ablehnst.
Ich bitte doch etws mehr um Respekt, wenn Du schon einen Sachverhalt als falsch deklarierst, sollte Du dich wengisten noch um eine sachliche Begründung bemühen.
Du verräst uns sicher wie Du mit a = P / (v * m) eine Beschleunigung aus dem Stand ermittelst. Solange hier keine sachlichen Argumente folgen stufe ich deinen Kommentar als unseriös ohne nenneswerten Inhalt ein. Ebenso verräst Du uns mit a = P / (v * m) wie Du hier den Beschleunigunsverlauf innerhalb einer einzelnen Übersetzung genau auflösen kannst.
Auch ein Punkt für Timmerings Jan (abgesehen von der Tatsache, dass die Formel korrekt lautet:
(2 * pi * r * rpm
/I * 60).
Und jetzt mal zum Wesentlichen:
Die beiden Fraktionen "Leistung" und "Drehmoment" stehen sich hier derart verbissen gegenüber, dass sie gar nicht mehr merken, dass beide Recht haben und lediglich dieselben physikalischen Zusammenhänge aus zwei verschiedenen Blickwinkeln betrachten.
In meiner beruflichen Tätigkeit habe ich ebenfalls schon nette Modelle zur Berechnung der Fahrzeugbewegung erstellt. Dabei habe ich tatsächlich, dem alten Newton folgend, ebenfalls den naheliegenden Weg über die Kraft respektive Drehmoment genommen. Letztlich wird ein Fahrzeug durch das Überschussmoment, welches am Rad anliegt, beschleunigt. Also das Moment, welches nach Abzug der zu überwindenden Roll- und Luftwiderstandsmomente übrig bleibt. Zur Vereinfachung lasse ich diese im Folgenden weg, betrachte also nur niedrige Geschwindigkeiten.
Dann ist die momentane Beschleunigung in einem festen Gang tatsächlich proportional zum Raddrehmoment und über die Getriebeübersetzung somit zum Motordrehmoment. Das erklärt einleuchtend, weshalb in höheren Gängen die Beschleunigung niedriger ausfällt.
So, nachdem ich jetzt der Momentenfraktion Recht gegeben habe, kommt nun die Leistungsfraktion dran:
Wann erreiche ich bei einer bestimmten Geschwindigkeit die höchste Beschleunigung? Nun, wie wir oben festgestellt haben dann, wenn das Radmoment am größten ist. Mit einer bestimmten Geschwindigkeit ist aber untrennbar eine bestimmte Raddrehzahl verbunden. mit dieser und dem Raddrehmoment lässt sich leicht die Radleistung ausrechnen. Also folgt ganz logisch, dass zur Erzielung einer hohen Beschleunigung die Radleistung möglichst hoch sein muss. Und das erreicht man, indem man die Getriebeübersetzung (Gang) so wählt, dass der Motor möglichst in seinem Leistungsmaximum betrieben wird.
Die Höchstgeschwindigkeit erreicht man dann, wenn das Gleichgewicht aus Fahrwiderständen und Antriebsleistung auf den Punkt der Motorhöchstleistung fällt.
Beide Fraktionen vergessen hier häufig den Einfluss des Getriebes, betrachten nur den Motor und diskutieren ständig aneinander vorbei. Dann kommt so etwas dabei heraus:
"Hmm sehr komisch, trotz der gleichen Leistung ist im 1. Gang die Beschleunigung größer als im 5. Gang. Wie kann das sein, es soll ja angeblich die Leistung das Fahrzeug beschleunigen?"
Bedenkt meine obigen Ausführungen und begrabt das Kriegsbeil.
Wie gesagt, ihr redet über das Gleiche, nur aus zwei unterschiedlichen Blickwinkeln. Der Physik dahinter ist das aber völlig egal. Sie ändert sich dadurch nicht.
657 Antworten
Zitat:
@FWebe schrieb am 22. Juli 2020 um 12:41:19 Uhr:
...
Die Aussage stimmt ja auch für die theoretische Höchstgeschwindigkeit.
Dafür muss die Zugkraft maximal sein und das ist nun mal bei Nennleistung der Fall.Wieder mal der Flugkörper als Beispiel, da hier kein Getriebe im Weg ist:
Die Höchstgeschwindigkeit erreicht man dort nur bei Nennleistung des Antriebs, weil nur dann der Schub maximal ist.Da F = P/ v wird die höchste Zugkraft bei Nennleistung erzielt und deshalb wird die theoretische Höchstgeschwindigkeit auch bei Nennleistung erreicht, da nur dann die Zugkraft maximal ist.
Es lässt sich ja einfach nachhalten:
a = (P/ v)/ m
Wenn
m = konstant
und
v = konstant
dann ist a ~ P.Der Zusammenhang ergibt sich beim Vergleich gestufter Gänge ganz von alleine:
v = 14 m/ s
100 Nm mit 3000 U/ min, sprich 31,41 kW
ergibt eine höhere Beschleunigung als
100 Nm mit 1500 U/ min, sprich 15,70 kW.
Die Zugkraft liegt im ersten Fall bei 2,24 kN
und im zweiten Fall bei 1,12 kN.Will man die Beschleunigung darstellen, berücksichtigt man noch die Masse.
m = 1000 kg
Damit ergibt sich im ersten Fall
a = 31,41 kW/ 14 m/ s/ 1000 kg = 2,24 m/ s^2
und im zweiten Fall
a = 15,70 kW/ 14 m/ s/ 1000 kg = 1,12 m/ s^2
Man sieht sehr gut, dass bei v = konstant a ~ P....
Aber doch nur, wenn m = 1.000 kg. Weil, meinen Golf, mit dessen Daten ich rumspiele, würde 1.400 kg haben. 😉
Ich habe mal gerechnet, bin deinen Weg gegangen und auch den von Duke711 oben.
OBACHT!
Als ich auf Abfahrt drückte, kam, Seite nicht gefunden. 😠
Offenbar hat MT auf "dem Server" einen Timer für den Datenaustausch eingebaut.
Wer einen langen Beitrag schreiben will oder dafür mehr Zeit braucht, sollte seinen Text unbedingt kopieren bzw. extern speichern bevor er auf Abfahrt drückt.
Ich schaute mir die Sache für 4.500, 5.800 und 6.500 im 1. und 6. Gang an.
1. G GÜ 16,71
6. G GÜ 3,07
r = 0,31715
3,05 anstatt Pi (da so in meiner Datenquelle und zum Abgleich)
4.500 = Ende Mmax 240 Nm
5.800 = Pmax 118 bei Vmax 220 im 6. Gang
6.500 = Ende Drehzahl, ebenso 118 kW angenommen, ging schneller sowie TL hält auch die Leistung oben.
...
1. Gang [m/s²]
4.500: 9,3
5.800: 7,5
6.500: 6,7
6. Gang [m/s²]
4.500: 1,7
5.800: 1,4 (Vmax)
6.500: (1,2)
An alle: Danke für die Nachhilfe. 🙂
VG myinfo
Zitat:
@myinfo schrieb am 22. Juli 2020 um 18:23:53 Uhr:
Aber doch nur, wenn m = 1.000 kg. Weil, meinen Golf, mit dessen Daten ich rumspiele, würde 1.400 kg haben. ??
Klar, nur wie gesagt, die Masse wird erst dann interessant, wenn du die tatsächliche Beschleunigung auch ausrechnen willst. Da sich die Masse aber während der Beschleunigung nicht nennenswert verändert, ist sie zur Betrachtung der relativen Beschleunigung nicht wichtig.
Dafür ist nur die Radleistung bzw. die Radzugkraft interessant. Mehr Leistung bedeutet mehr Radzugkraft und führt deshalb zu einer höheren Beschleunigung.
Für die höchste Beschleunigung stellt sich entsprechend nur die Frage, wie man die Radzugkraft maximiert, sprich welche Übersetzung den meisten Benefit bringt und die Frage wird mit der Leistung beantwortet.
Rechne dir das mal für 40 km/ h im 1. - 4. Gang durch. Im 1. wird sehr wahrscheinlich immer die höchste Leistung und damit auch die höchste Radzugkraft erzielt.
Zitat:
@myinfo schrieb am 22. Juli 2020 um 18:23:53 Uhr:
Wer einen langen Beitrag schreiben will oder dafür mehr Zeit braucht, sollte seinen Text unbedingt kopieren bzw. extern speichern bevor er auf Abfahrt drückt.
Das ist leider ein bekanntes Problem, was die zuständigen Leutchen seit geraumer Zeit nicht in den Griff bekommen. 🙁
Zahlen sind ja immer schön und theoretische Abhandlungen !
auch die Achsübersetzung macht das Raddrehmoment aus,
in der Praxis !
Man könnte ja auch einmal die theoretischen Zahlen hier
in eine Graphik für normalsterbliche Menschen Umsetzen,
damit man es sieht,
sonst sind Wir im einem Symposium für Außerirdische .
so 2 Beispiele ,für Normalos .
Ähnliche Themen
Zitat:
@FWebe schrieb am 22. Juli 2020 um 18:50:37 Uhr:
Dafür ist nur die Radleistung bzw. die Radzugkraft interessant. Mehr Leistung bedeutet mehr Radzugkraft und führt deshalb zu einer höheren Beschleunigung.
Das ist nach wie vor falsch und wird auch nicht richtig, ich glaube ich habe jetzt mind. zum 3. mal die Gleichung hier gepostet, siehe oben, kann doch nicht so schwer sein oder doch?
Hier die nochmal die Excel mit den Grafiken:
https://www.motor-talk.de/.../...auchs-von-fahrweise-t6887298.html?...
In den Grafiken oder in der o. Grafik von Rosi03677 ist doch ganz deutlich zu erkennen wo jeweils das größte Raddrehmoment und somit die Zugkraft ist, jeden falls nicht bei der max. Leistung...
Mich würde mal brennend interessieren wie Du überhaupt die Beschleunigung aus dem Stand ausrechen willst, auch etwa mit a = P * v^-1 / m ?
Man muss die Radzugkraft nicht absolut sehen, sondern im Verhältnis zur Geschwindigkeit.
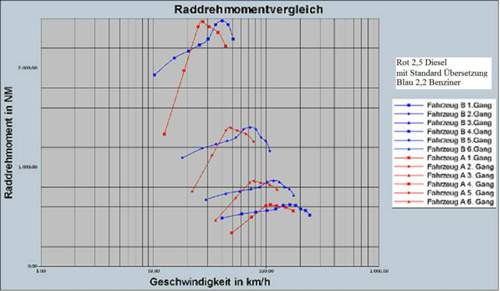
Auch sehr Verständlich gemacht,bei MT
https://www.motor-talk.de/.../Attachment.html?attachmentId=673475
Zitat:
@rosi03677 schrieb am 22. Juli 2020 um 21:54:11 Uhr:
Auch sehr Verständlich gemacht,bei MT
https://www.motor-talk.de/.../Attachment.html?attachmentId=673475
Dann solltest du es verstehen.
Warum doch nicht?
Zitat:
@Duke711 schrieb am 22. Juli 2020 um 11:39:42 Uhr:
Zitat:
@FWebe schrieb am 22. Juli 2020 um 10:24:31 Uhr:
Wenn du die Masse berücksichtigen willst, sieht die Gleichung so aus:
a = (P/ v)/ mDie Gleichung ist aber nicht gültig
Problem 1.
Bechleunigung aus dem Stand:
a = (200000 / 0) / 1600 = 0
Weit daneben. Du verwechselt "mal Null" mit "durch Null".
Merke: wer mit Mathematik Dinge beweisen will, sollte sie zuerst mal selbst richtig anwenden. 😎
Zitat:
Problem 2.
Die Gleichung beschreibt die ideale Leistungshyperbel, berücksichtigt also nicht die Übersetzungsabstufungen.
Das tut dein heiliges F = m * a genau so wenig.
Zitat:
Außerdem löst diese Gleichung nicht die Zeitinkremente der Beschleunigung auf, sondern nur einen Durchschnitt.
Falsch. In diesem Punkt gibt es exakt Null Unterschied zwischen den beiden Gleichungen. Beide gelten für jeden beliebigen Zeitpunkt einzeln, wenn man korrekt zeitabhängige Werte einsetzt; und sie gelten gemittelt, wenn man geeignete Mittelwerte bzw. Konstanten vorliegen hat.
Zitat:
Richtig ist diese Gleichung hier und wird über die Leistung, 200 kW, gerechnet:
F = m * a
Die ist weder richtiger noch falscher, sondern schlicht sie selbe Gleichung in anderer Darstellung.
Zitat:
a ={[(P * 60) / (2 * rpm* pi)] * I} / (r * m)
Und wenn dir jetzt noch klar wird, dass (2 * pi * r * rpm * I * 60) nichts anderes als eine komplizierte Schreibweise für die Geschwindigkeit ist, steht da:
a = P / (v * m)
Was, oh Wunder, genau die Gleichung ist, die so vehement ablehnst.
Zitat:
Leistung ist übrigens nur ein Produkt und somit eine imaginäre Größe.
Das ist ein komplettes Null-Argument. Drehmoment ist auch nur ain Produkt, also auch nur eine imaginäre Größe. Kraft übrigens auch. Wenn du das konsequent durchziehst, ist die ganze Welt imaginär und nichts bleibt übrig.
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Zitat:
@Duke711 schrieb am 22. Juli 2020 um 11:39:42 Uhr:
Die Gleichung ist aber nicht gültig
Problem 1.
Bechleunigung aus dem Stand:
a = (200000 / 0) / 1600 = 0
Weit daneben. Du verwechselt "mal Null" mit "durch Null".
Ich glaube Du verwechselst hier was. Aber sicher kommt hier noch ein Lösungsvorschlag wie man die o.g. Gleichung lösen kann, die ist übrigens so richtig. Mit Doppelbrüchen scheinst Du wohl so deine Schwierigkeiten zu haben?
Zitat:
@Timmerings Jan [url=https://www.motor-talk.de/.../...auchs-von-fahrweise-t6887298.html?...]schrieb am 22. Juli 2020 um 22:03:29
Merke: wer mit Mathematik Dinge beweisen will, sollte sie zuerst mal selbst richtig anwenden. 😎
Bitte die o.g. Gleichung lösen und eine reelle Zahl aufzeigen, danke.
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Zitat:
Problem 2.
Die Gleichung beschreibt die ideale Leistungshyperbel, berücksichtigt also nicht die Übersetzungsabstufungen.
Das tut dein heiliges F = m * a genau so wenig.
Tut es nicht, sachliche Argumente scheinen dir nicht zu liegen?
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Zitat:
Außerdem löst diese Gleichung nicht die Zeitinkremente der Beschleunigung auf, sondern nur einen Durchschnitt.
Falsch. In diesem Punkt gibt es exakt Null Unterschied zwischen den beiden Gleichungen. Beide gelten für jeden beliebigen Zeitpunkt einzeln, wenn man korrekt zeitabhängige Werte einsetzt; und sie gelten gemittelt, wenn man geeignete Mittelwerte bzw. Konstanten vorliegen hat.
Das kannst Du uns sicherlich ausführlich erklären. Die DGL habe ich übrigens nicht umsonst hier aufgeführt. Bitte eine DGL über P aufstellen mit einer Beschleunigung aus dem Stand.
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Zitat:
a ={[(P * 60) / (2 * rpm* pi)] * I} / (r * m)
Und wenn dir jetzt noch klar wird, dass (2 * pi * r * rpm * I * 60) nichts anderes als eine komplizierte Schreibweise für die Geschwindigkeit ist, steht da:
a = P / (v * m)
Was, oh Wunder, genau die Gleichung ist, die so vehement ablehnst.
Ich bitte doch etws mehr um Respekt, wenn Du schon einen Sachverhalt als falsch deklarierst, sollte Du dich wengisten noch um eine sachliche Begründung bemühen.
Du verräst uns sicher wie Du mit a = P / (v * m) eine Beschleunigung aus dem Stand ermittelst. Solange hier keine sachlichen Argumente folgen stufe ich deinen Kommentar als unseriös ohne nenneswerten Inhalt ein. Ebenso verräst Du uns mit a = P / (v * m) wie Du hier den Beschleunigunsverlauf innerhalb einer einzelnen Übersetzung genau auflösen kannst.
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Zitat:
Leistung ist übrigens nur ein Produkt und somit eine imaginäre Größe.
Zitat:
@Timmerings Jan schrieb am 22. Juli 2020 um 22:03:29 Uhr:
Das ist ein komplettes Null-Argument. Drehmoment ist auch nur ain Produkt, also auch nur eine imaginäre Größe. Kraft übrigens auch. Wenn du das konsequent durchziehst, ist die ganze Welt imaginär und nichts bleibt übrig.
Auch das ist falsch. Kraft ist eine direkt zu messende Größe. Die Leistung wird nur berechnet. Das ist ein bedeutender Unterschied.
So ich das hier mitbekommen habe, kamen von dir hier übrigens im Thread kaum sachliche Argumente, solltest Du vielleicht mal daran arbeiten.
Du erstellst und sicher ein Beispiel mit einem F (v) oder a (v) Diagramm wie in diesem Beispiel hier:
https://www.motor-talk.de/.../Attachment.html?attachmentId=673475
Über a = P / (v * m).
Zitat:
@Duke711 schrieb am 22. Juli 2020 um 20:42:20 Uhr:
Zitat:
@FWebe schrieb am 22. Juli 2020 um 18:50:37 Uhr:
Dafür ist nur die Radleistung bzw. die Radzugkraft interessant. Mehr Leistung bedeutet mehr Radzugkraft und führt deshalb zu einer höheren Beschleunigung.
Das ist nach wie vor falsch und wird auch nicht richtig, ich glaube ich habe jetzt mind. zum 3. mal die Gleichung hier gepostet, siehe oben, kann doch nicht so schwer sein oder doch?
...
Darf ich das Missverständnis auflösen?
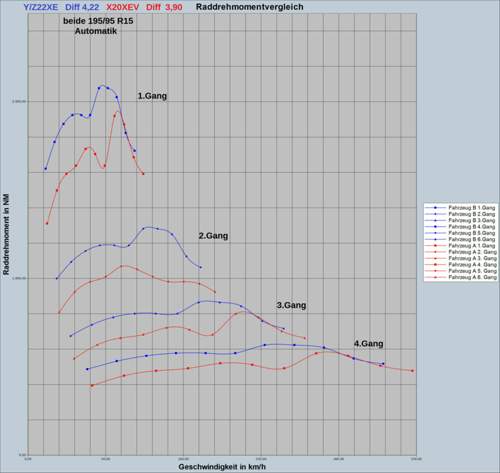
Radzugkraftdiagramm => Grafik mit Lösung anbei
x-Achse in km/h
y-Achse in N
Duke711
Er schaut unabhängig vom Tempo nach dem Maximum "= Berggipfel" und liest den Wert auf der Y-Achse ab = grüner Pfeil in der Grafik.
An diesem Punkt ist die Radzugkraft am allerhöchsten.
FWebe
Er betrachtet eine bestimmte Geschwindigkeit x.
An diesem Punkt schaut er, in welchem Gang die Radzugkraft am höchsten ist = blauer Pfeil.
Anbei die Grafik
Duke711 = grüner Pfeil
FWebe = blauer Pfeil
VG myinfo
Ich weiß das Fwebe nur die Leistungshyperbel, also die rot gestrichelte Linie betrachtet. Nur ist das die ideale Beschleunigung stehts ohne Getriebe. Auch spiegelt diese nicht die Maximalbeschleunigung wieder. Man sieht ja in den a (v) oder F (v), das stets das maximale Motordrehmoment die pro Zeitinkrement die maximale Bechleungiung hervor ruft und nicht P.
Siehe Grafik
https://i.ebayimg.com/00/s/OTIwWDE2MDA=/z/SfoAAOSw-9lfFKPx/$_10.JPG
Oder man könnte, Quelle:
https://www.motor-talk.de/.../Attachment.html?attachmentId=673475
Die Zugkraft y Abzisse einfach 1:1 gegen m/s² tauschen der Kurvenverlauf würde sich nicht ändern und folgt der Motordrehmomentkurve und nicht der P-Kurve. Somit hat stets das maximale Motordrehmoent und Zugkraft stets die höchste Beschleunigung. Das was wohl auch ein Herr Timmerings Jan nicht verstanden hat.
Zitat:
@Duke711 schrieb am 23. Juli 2020 um 01:21:05 Uhr:
Ich weiß das Fwebe nur die Leistungshyperbel, also die rot gestrichelte Linie betrachtet.
Wenn du das glaubst, dann weißt du tatsächlich nicht, was ich meine.
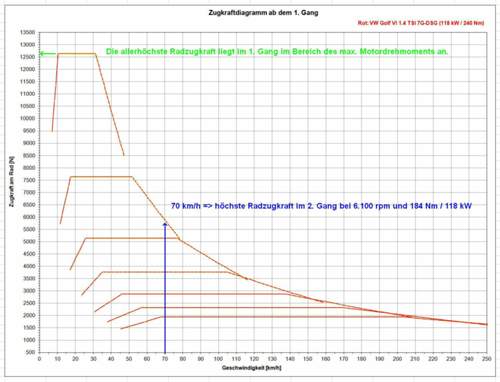
Nimm das Zugkraftdiagramm und sag mir, in welchem Gang die höchste Zugkraft bei 30 km/ h erzielt wird und rechne dann die dabei erzielte Leistung aus.
Man sieht es auch in deinem Diagramm, dass die Zugkraft dann am höchsten ist, wenn die höchste Leistung bei einer bestimmten Geschwindigkeit erzielt wird.
Das dem so ist, ist wenig verwunderlich, da nach F = P/ v für v = konstant P nun mal maximal werden muss, um ein maximales F zu erzielen.
Im Idealfall wird die Nennleistung erzielt. Grundsätzlich gilt aber, dass für v = konstant F ~ P, sprich wenn die Leistung steigt, steigt auch die Zugkraft.
Wäre dem nicht so, brächte Runterschalten z.B. niemals einen Vorteil bei der Beschleunigung.
https://www.motor-talk.de/.../Attachment.html?attachmentId=673475
Bei 30 km/h ist hier die höchste Zugkraft und somit Beschleunigung stets beim höchsten Motordrehmoment der entsprechenden Drehzahl bei 30 km/h und nicht die Leistung.
Wie errechnest Du mit a = P / (v * m) die Beschleunigung aus dem Stand, vermisse immer noch eine Beispielrechnung?
Ich wiederhole die Aufgabe gerne nochmal:
Nimm das Zugkraftdiagramm und sag mir, in welchem Gang die höchste Zugkraft bei 30 km/ h erzielt wird und rechne dann die dabei erzielte Leistung aus.
Dein eigenes Diagramm ist doch der beste Beleg dafür, dass bei 30 km/ h im 1. Gang die höchste Leistung und deshalb auch im ersten Gang die höchste Zugkraft bei 30 km/ h erzielt wird.
Anhang:
Um es abzukürzen bekommst du die Lösung gleich dazu.
Im ersten Gang werden bei 30 km/ h ca. 63 kW erzielt.
Im zweiten Gang hingegen ca. 36 kW.



![Avatar von Go}][{esZorN](https://img.motor-talk.de/media/user/goeszorn-u4959/0_original.gif)