Einfluss Radgewicht auf Beschleunigung
Am Vergleich zwischen dem 340i und dem Jaguar XE S in der Auto Zeitung Nr.19 vom 26.8.2015 erkennt man sehr schön welchen negativen Einfluss schwere Räder auf die Beschleunigung haben.
Mit 18 Zoll Michelin Super Sport Bereifung beschleunigt der 326PS starke und 1632kg schwere BMW um 2.2s schneller auf 200km/h als der auf 19Zoll stehende 14ps stärkere 340ps und 1710kg schwere Jaguar mit schwerer Dunlop Sport Maxx RT Bereifung - beide mit 450Nm und identischer 8Gang ZF Sportautomatik.
2.2s ist schon eine Hausnummer und kann nicht nur auf die überlegene BMW Motorentechnik geschoben werden 😉
Beste Antwort im Thema
Zitat:
@ManfredBlair schrieb am 14. September 2015 um 08:26:45 Uhr:
Ich behaupte das die unterschiedlich großen Räder zumindest 1s ausmachen, d.h. Bei identischer 19Zoll Bereifung des BMW beschleunigt er 1s langsamer auf 200km/h.Zitat:
@MartinBru schrieb am 14. September 2015 um 00:46:22 Uhr:
Bei all den Unterschieden bei den technischen Daten haben die Räder wohl den kleinsten Einfluss auf die Fahrleistungen.
Schön, dass hier mal wieder ohne jeglichen Nachweis "behaupet" wird und Meinungen als Tatsachen ausgegeben werden.
Ein kleines bißchen genaues Lesen, Nachdenken und Rechnen hilft.
1.) Der BMW tritt in diesem Test nicht mit Originalbereifung (225/50 R17) an.
2.) Die Reifen beider Testfahrzeuge sind an Vorder- und Hinterachse jeweils gleich breit (225 bzw. 255). Die Flankenhöhe beim BMW beträgt vorne 101,25 mm, hinten 102 mm, beim Jaguar vorne 90 mm, hinten 89,25 mm. Bei einem gleichen Reifenfabrikat dürften die Reifen des Jaguars also leichter sein als die des BMW.
3.) Die 19 Zoll Felgen werden etwas schwerer als baugleiche 18 Zoll Felgen sein. In Verbindung mit dem geringeren Reifengewicht dürfte es bei +- Null herauskommen.
4.) Die vorderen Felgen des BMW sind 8 Zoll breit, die des Jaguar nur 7,5! Die vorderen Felgen beider Fahrzeuge dürften ungefähr das gleiche wiegen.
Der Gewichtsunterschied beider Radsätze sollte unter 1 kg liegen. Das als Begründung für die bessere Beschleunigung des BMW auf 200 km/h halte ich für sehr gewagt.
139 Antworten
Das kann ProE sicher in ein Diagramm schreiben. Getriebe, Kupplung, ... kann hier vernachlässigt werden, da beide Fahrzeuge für einen Vergleich identisch sein müssen. Macht's nicht zu kompliziert.
Zitat:
@ManfredBlair schrieb am 13. September 2015 um 23:36:20 Uhr:
Beide Autos haben einen cw Wert von 0.26.
Der Wert alleine sagt ungefähr so viel aus wie die Schuhgröße des Fahrers. 😁
Zitat:
@ManfredBlair schrieb am 13. September 2015 um 23:12:44 Uhr:
2.2s ist schon eine Hausnummer und kann nicht nur auf die überlegene BMW Motorentechnik geschoben werden 😉
Ich traue BMW zu, dass der 5er hinsichtlich des cw x A - Wertes günstiger ist, gerade bei Messungen in sehr hohen Geschwindigkeitsbereichen macht das sehr viel aus. Generell sind BMW - Fahrzeuge aber sehr gut beschleunigend, in der Auto Zeitung wurde neulich ein BMW 335i mit einem Ford Mustang 5.0 V8 verglichen, trotz über 100 PS Leistungsunterschied und ähnlichem Leergewicht war die Beschleunigung fast identisch.
Zitat:
@softwarefriedl schrieb am 19. September 2015 um 13:31:12 Uhr:
Mustang 5.0 ist zum anhören, ned zum heizen
Wofür dann >400 PS?!
Ähnliche Themen
Zitat:
@Bartman schrieb am 19. September 2015 um 13:58:11 Uhr:
Wofür dann >400 PS?!Zitat:
@softwarefriedl schrieb am 19. September 2015 um 13:31:12 Uhr:
Mustang 5.0 ist zum anhören, ned zum heizen
Marketing
Du enttäuschst mich. So, wie Du Dich hier darstellst, hätte ich etwas mehr technischen Sachverstand erwartet. Schade.
Zitat:
@ManfredBlair schrieb am 19. September 2015 um 00:32:45 Uhr:
Du hast zwei Fehler gemacht:Zitat:
@Rael_Imperial schrieb am 18. September 2015 um 21:33:26 Uhr:
Ich habe jetzt kein Simulationsprogramm zur Hand, nicht mal einen Taschenrechner. Geht aber auch ohne.Zunächst werden die rotatorischen Massen den translatorischen zugeschlagen. Dazu benötigt man das Quadrat des Radradius. Der liegt bei ca. 0,3 irgendwas m. r*r ist also ungefähr 0,1 m^2. Aus I1 = 1,13 kg m^2 werden so 11,3 kg, aus I2 = 1,43 kg m^2 werden 14,3 kg. Delta 3 kg für ein Rad, 12 kg für vier Räder. Aus der rein translatorischen Fahrzeugmasse von 1800 kg werden im ersten Fall also 1845,2 kg, im zweiten Fall 1857,2 kg.
Der Einfluss von 0 - 200 km/h??
Pfffff .........1. die Differenz der beiden reduzierten Fahrzeugmassen muss logischerweise größer als 4 x 3 = 12 kg sein, da das Gewicht der 17Zoll und 18Zoll Räder unterschiedlich ist.
Du hattest in Deiner "Aufgabenstellung" die Radmasse nicht ausdrücklich erwähnt, sondern nur das Trägheitsmoment. Daher habe ich mich auch nur auf dieses bezogen.
Ja mei, dann addiere halt noch 6 kg für die vier Räder dazu. Und, was ändert das jetzt großartig?
Zitat:
2. die reduzierten Fahrzeugmassen sind viel größer als die zusätzlichen 45.2 bzw. 57.2kg - du hast den kompletten restlichen Term des reduzierten Massenträgheitsmomentes bestehend aus Sekundärübersetzung, Achsantrieb, Motor, Gangübersetzung, Kupplung und Bremse weggelassen.
Ich dachte, Du hättest Ahnung. Wenn die Räder geändert werden, dann ändert sich am Rest des Triebstranges gar nichts.
Es ist sogar so, dass durch die genannten weiteren Komponenten sich der Einfluss der Räder noch verringert, da die "virtuelle" Fahrzeugmasse durch sie noch ansteigt. Also muss man das erhöhte Trägheitsmoment der Räder nicht nur auf 1800 kg, sondern auf vielleicht 1900 kg (nicht gerechnet, sondern einfach als Beispiel) beziehen.
Zitat:
Weiters fehlt noch immer die Bewegungsgleichung um die tatsächlichen Beschleunigungszeiten ermitteln zu können.
Ich habe doch bereits geschrieben, dass ich mich intensiv mit Simulationen beschäfftige. Deshalb erzählst Du mir nichts Neues. Ich kenne die Gleichungen. Um die ging es im Thread aber nicht, sondern lediglich darum, wie sich ein anderer Felgendurchmesser auswirkt. Die komplette Formel hatte ich hier übrigens bereits vor ein paar Jahren gepostet. Vielleicht findest Du sie ja in der Suche.
Zitat:
Hierbei ist aufgrund der gangabhängigen Massenfaktoren eine stückweise Integration erforderlich (in deiner Tabelle passen die Größenordnungen der Massenfaktoren übrigens nicht mit den Gangübersetzungungen von deinem Beispiel überein)
Stückweise im Sinne von "nach einem Gangwechsel mit anderen Parametern (Übersetzungen)"?
Ja! Selbstverständlich. Und?
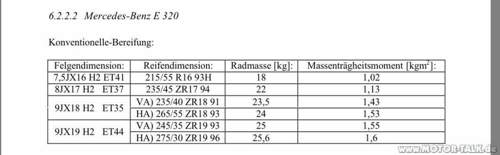
Es ist übrigens nicht meine Tabelle und in ihr stehen Beispielwerte. Sie hat keinen direkten Bezug zu den Fahrzeugdaten auf der Seite davor. Wie soll man ihre Richtigkeit überprüfen, ohne die Eingangsdaten zu kennen?
Zitat:
Erhöht sich beispielsweise der Massenfaktor in jedem Gang um ein paar Prozent hast dies entsprechend negative Auswirkungen im Zehntelbereich bei der Beschleunigung!
Bei dem ausgewählten Beispiel zwischen den 17zoll und 18zoll Rädern mag der Unterschied nicht so extrem sein, bei einem Vergleich zwischen 16zoll NonRFT und 20 Zoll RFT sieht es schon anders aus.
Und hier zeigt sich jetzt Dein Verständnisproblem:
Da die Fahrzeugbeschleunigung interessiert, macht es Sinn, alle Massen und Trägheitsmomente auf die Radseite des Antriebsstranges zu beziehen, nicht auf die Motorseite. Alles vor dem Getriebe (Motor, ZMS, Kupplung) wird mit dem Quadrat der Gesamtübersetzung auf die Radseite umgerechnet. Entsprechend alles zwischen Getriebe und Differential mit dem Quadrat der Achsübersetzung. Und hinter dem Differential wird nichts mehr umgerechnet, da es bereits auf Raddrehzahl ist.
Das heißt, dass der Radeinfluss eben nicht gangabhängig ist. Wieso sollte er es auch sein?? Der gangabhängige Massenfaktor beinhaltet alles, was rotiert, aber eben nicht die Räder!
Das geht übrigens eindeutig aus den Formeln hervor, die Du ebenfalls in Deinem Beitrag gepostet hast.
Jetzt muss ich aber schmunzeln:
Du hast bei der Anwendung deiner Formeln zwei grundlegende Fehler gemacht und unterstellst mir fehlenden Sachverstand?
Weiters bist du nie auf die eigentliche Fragestellung - nämlich der Beschleunigungszeit - eingegangen, sondern hast lediglich deine Formeln (falsch) ausgerechnet.
Bezüglich deiner unterstellten Ahnungslosigkeit:
Es ist mir schon klar, dass sich der restliche Antriebsstrang nicht ändert, wenn man die Räder austauscht, trotzdem gehört er in die Betrachtung mit einbezogen - schon allein aus dem Grund weil er quantitativ den größten Anteil des Zählers beim gangabhängigen Massenfaktor ausmacht!
Worin liegt mein Verständnisproblem?
Habe vollkommen richtig geschrieben, dass sich der gangabhängige Massenfaktor (welcher u.a. vom Massenträgheitsmoment der Räder abhängt) in jedem Gang um ein paar Prozent aufgrund des höheren Massenträgheitsmomentes der größeren Räder erhöht.
Das alle im mathematischen Modell vorkommenden Massenträgheitsmomente auf die Radseite bezogen werden, versteht sich von selbst.
Swoooosch. Kabuuuummm.
*Plop*
Jungs, ist das nicht vollkommen egal? So lange Manni und der Imperator beide Freude am Fahren haben ist doch alles gut!
Zitat:
@ManfredBlair schrieb am 19. September 2015 um 21:54:25 Uhr:
Jetzt muss ich aber schmunzeln:
Du hast bei der Anwendung deiner Formeln zwei grundlegende Fehler gemacht und unterstellst mir fehlenden Sachverstand?
Ja, denn ich habe bereits widerlegt, dass ich zwei grundlegende Fehler gemacht habe. Und Du behauptest nur ständig, ich würde Fehler machen, kannst sie aber weder korrigieren noch gar eigene Fakten dagegen stellen.
Zitat:
Weiters bist du nie auf die eigentliche Fragestellung - nämlich der Beschleunigungszeit - eingegangen, sondern hast lediglich deine Formeln (falsch) ausgerechnet.
Die tatsächliche Beschleunigungszeit könnte ich berechnen, wenn ich mir sämtliche Daten der beiden Fahrzeuge besorge und in mein Simulationsmodell eingebe. Mal abgesehen davon, dass ich für den Jaguar weder die Gang- noch die Achsüberstzung gefunden habe, habe ich schlicht weder Zeit noch Lust auf den Aufwand. Und wie ich bereits sagte, als guter Ingenieur bin ich auch abseits irgendwelcher Computerberechnungen in der Lage, Werte auf ihre Plausibilität hin zu bewerten. Und eine um zwei Sekunden bessere Beschleunigungszeit ausschließlich auf einen anderen Felgen- (nicht: Rad-)durchmesser zurückzuführen, ist schlicht unplausibel.
Zitat:
Worin liegt mein Verständnisproblem? Habe vollkommen richtig geschrieben, dass sich der gangabhängige Massenfaktor (welcher u.a. vom Massenträgheitsmoment der Räder abhängt) in jedem Gang um ein paar Prozent aufgrund des höheren Massenträgheitsmomentes der größeren Räder erhöht.
Siehst Du, das ist der Unterschied zwischen uns: Du vermutest und behauptest, ich rechne und belege:
Ich beziehe mich auf das bereits verwendete Beispiel (siehe Anhang). Ausgehend von Jr1 = 1,2 kg m² habe ich Jr2 = 1,519 kg m² gesetzt. Dies entspricht der gleichen prozentualen Erhöhung wie Dein Beispiel mit 1,13 und 1,43 kg m². Das Mehrgewicht der vier Räder habe ich mit zusammen 6 kg angesetzt.
Mit dem ersten (Jr1) und zweiten Radsatz (Jr2) ergeben sich folgende reduzierte Trägheitsmomente (zweiter Index = Gang):
J1_1 = 15,70 kg m², J2_1 = 16,98 kg m²
J1_2 = 11,84 kg m², J2_2 = 13,11 kg m²
J1_3 = 9,14 kg m², J2_3 = 10,42 kg m²
J1_4 = 7,72 kg m², J2_4 = 8,99 kg m²
J1_5 = 6,89 kg m², J2_5 = 8,17 kg m²
J1_6 = 6,48 kg m², J2_6 = 7,76 kg m²
Damit wird der Drehmassenzuschlagsfaktor e ermittelt:
e1_1 = 1,132 e2_1 = 1,142
e1_2 = 1,099 e2_2 = 1,110
e1_3 = 1,077 e2_3 = 1,087
e1_4 = 1,065 e2_4 = 1,075
e1_5 = 1,058 e2_5 = 1,068
e1_6 = 1,054 e2_6 = 1,065
Daraus erhält man schließlich die effektive Fahrzeugmasse (e*m):
m1_1 = 1358 kg, m2_1 = 1377 kg
m1_2 = 1319 kg, m2_2 = 1338 kg
m1_3 = 1292 kg, m2_3 = 1311 kg
m1_4 = 1278 kg, m2_4 = 1297 kg
m1_5 = 1269 kg, m2_5 = 1288 kg
m1_6 = 1265 kg, m2_6 = 1284 kg
Wie man sieht, beträgt die Erhöhung der effektiven (virtuellen) Fahrzeugmasse 19 kg. Und zwar unabhängig vom Gang! Und davon gehen 6 kg auf die tatsächliche Masse und 13 kg auf das erhöhte Radträgheitsmoment.
Und das soll ernsthaft die Begründung für eine um zwei Sekunden schlechtere Beschleunigung sein??
Und wieder wurde die Aussage von mir bestätigt, dass sich der gangabhängige Massenfaktor in jedem Gang um ein paar Prozent erhöht.
Oder habe ich irgendwo geschrieben, dass sich der gangabhängige Massenfaktor in jedem Gang unterschiedlich erhöht?
Bitte genau lesen und nicht zwanghaft nach Fehlern suchen.
Weiters wurde nie behauptet, dass sich die 2s kürzere Beschleunigungszeit des BMW´s rein aufgrund der unterschiedliche schweren Rädern ergibt.
Der 340i wurde in einer anderen Autozeitschrift auf der Rolle mit über 340Ps gemessen.
Die kürzere Beschleunigungszeit ergibt sich also aus einer Kombination von Motorleistung, Massenträgheitsmoment der Räder und dem Luftwiderstandsbeiwert.
Zitat:
@ManfredBlair schrieb am 19. September 2015 um 23:39:25 Uhr:
Und wieder wurde die Aussage von mir bestätigt, dass sich der gangabhängige Massenfaktor in jedem Gang um ein paar Prozent erhöht.
Du drehst es Dir auch immer so zurecht, wie es gerade am besten passt.
Erst behauptest Du ständig, dass meine Formeln und Berechnungen falsch seien, und dann bestätigen sie plötzlich das, was Du angeblich schon immer gesagt hast.
*Kopfschüttel*
Zitat:
Weiters wurde nie behauptet, dass sich die 2s kürzere Beschleunigungszeit des BMW´s rein aufgrund der unterschiedliche schweren Rädern ergibt.
Der 340i wurde in einer anderen Autozeitschrift auf der Rolle mit über 340Ps gemessen.
Die kürzere Beschleunigungszeit ergibt sich also aus einer Kombination von Motorleistung, Massenträgheitsmoment der Räder und dem Luftwiderstandsbeiwert.
Was interessiert mich mein Geschwätz von gestern??
Zitat:
@ManfredBlair schrieb am 13. September 2015 um 23:12:44 Uhr:
Am Vergleich zwischen dem 340i und dem Jaguar XE S in der Auto Zeitung Nr.19 vom 26.8.2015 erkennt man sehr schön welchen negativen Einfluss schwere Räder auf die Beschleunigung haben.
Mit 18 Zoll Michelin Super Sport Bereifung beschleunigt der 326PS starke und 1632kg schwere BMW um 2.2s schneller auf 200km/h als der auf 19Zoll stehende 14ps stärkere 340ps und 1710kg schwere Jaguar mit schwerer Dunlop Sport Maxx RT Bereifung - beide mit 450Nm und identischer 8Gang ZF Sportautomatik.
Zitat:
@ManfredBlair schrieb am 16. September 2015 um 13:06:47 Uhr:
In dem konkreten Fall beträgt der Nachteil aufgrund der größeren 19 Zoll felgen und dem damit verbundenen höheren Massenträgheitsmoment der Räder (mehr Masse am äußeren Bereich des Rades) ca. 50-100kg fiktives Mehrgewicht des Fahrzeuges.
Dies allein rechtfertigt natürlich nicht die 2.2s langsamere Beschleunigung.
Der BMW Motor ist schon ein toller Motor, wo am Rad mehr Leistung ankommt als beim Mitbewerb 😉
Hier nochmal zur Erinnerung - die 50-100kg Mehrgewicht beruhen auf dem Faktor 7 aus dem Rennsport.
Anbei ein mathematisches Modell zur Simulation der Beschleunigungszeit.
Werde schauen das ich demnächst Ergebnisse für unterschiedliche Räder bekomme.
Dann sieht man genau, welchen quantitativen Einfluss bzw. wieviel Zehntel schwere Räder auf ein 0815 Fahrzeug haben.
In der Praxis treten dann natürlich noch zusätzliche Effekte auf, welche in dem mathematischen Modell nicht berücksichtigt werden können.
Manni, hast du noch ein paar Ideen wir man den Fünfer leichter macht?
Ich hab ja nun die schweren Pianoleisten gegen die Carbonleisten getauscht. Der Wagen ist nun etwas flinker und braucht etwas weniger Sprit! Ich glaub so in 1 Millarde km hab ich das Geld wieder raus. Aber das kann man doch auch genau ausrechnen?