Sinn und Unsinn der Plug-in Hybiden
Ich habe lange über dieses Thema nachgedacht. Vor einigen Tagen habe ich dann den Testbericht zum neuen Touareg R gesehen und ich muss meine Gedanken jetzt loswerden! Ich weiß, es wird die Geister spalten, aber so ist das eben.
Ich frage mich, ob die Leute sich eigentlich wirklich Gedanken machen was welchen Sinn solche Modelle überhaupt erfüllen sollen und was das vor allem umwelttechnisch bedeutet? Solche Autos sollen ein Bindeglied zwischen Verbrenner und Elektroantrieb darstellen und fahrerisch das Beste aus den beiden Welten vereinen. Das tun sie ohne jeden Zweifel. Sollten sie eigentlich. Aber bei einem Touareg R hört der Spaß auf. Da kommt der exakt gleiche Akku rein wie bei einem A3 E-tron. Ernsthaft?? So eine fette Kiste mit einem verhältnismäßig so winzigen Akku...? Das Auto ist langsamer als der eingestellte V8 Diesel und verbraucht auch noch mehr. Bravo! Das ist sinnvoller Fortschritt!
Warum haben alle Plug-in Hybriden im Konzern den selben Akku, egal wie groß und schwer sie sind?? Das macht je mehr die Fahrzeugmasse ansteigt umso weniger Sinn!
Plug-in Hybriden switchen je nach Fahrmodus intelligent zwischen elektrisch und Verbrenner. Wenn Leistung benötigt wird arbeiten die beiden Systeme im Verbund. Wie gut kann es für einen Verbrenner sein, wenn er kalt ist und bei einem Kickdown gleich sofort weit hochdrehen muss, um 30 Sekunden später abgeschaltet zu werden, weil es dann elektrisch weitergeht? Wie oft muss dann bei verhältnissmäßig viel häufigeren Kaltstarts / Kurzstrecke des Verbrennermotors aufgrund der hybriden Fahrweise das Motoröl gewechselt werden? Wird der Verbrennermotor etwa selbst wenn er aus ist aufgeheizt um die Betriebstemperatur zu erreichen? Wenn es so ist, bitte belehrt mich...
Abgesehen davon, möchte ich aber auch die Gedanken weiterlaufen lassen... was passiert mit diesen Fahrzeugen wenn sie altern?
Wie lange will ein Käufer eines solchen KFZ sein Auto denn fahren? 3 Jahre, 5, 10? Was dann? Was passiert dann? Ich versuche ein Beispiel zu beschreiben, welches gar nicht mal so unwahrscheinlich ist:
Irgendwann wird die Leistung des Akku nachlassen. Was kostet so ein Akku? 10, 15, 20 K? Ich denke auf jeden Fall über der Schmerzgrenze der meisten Besitzer... Bei einem A6/A7 TFSIe Quattro ist der Elektromotor ja meines Wissens mit in der S-Tronic verbunden. Die S-Tronic, wie auch der Akku werden nach vielleicht 10 Jahren oder 200.000 km hinüber sein (vielleicht früher, oder auch viel später) und eines Austausches bedürfen. Was jetzt schon bei einem normalen Verbrenner äußerst kostspielig ist, wird bei diesen Hybriden ohne Zweifel bei nicht mal ganz so alten Fahrzeugen zu einem wirtschaftlichen Totalschaden führen und auf dem Müll landen! Ja, jedes Auto erreicht mal sein Ende, aber vor 10 Jahren ist man mit einem A6 4F Diesel auch problemlos 300.000 gefahren - und konnte ihn zu 90% noch so benutzen wie am Tag der Abholung! Ob das mit einem halbtoten Akku auch noch so klappt bei einen Pluginhybriden? Im Verhältnis zu einem reinen Eletrofahrzeug mit einem weit größeren Akku muss der im Verhältnis viel kleinere Plug-in Hybriden Akku viel öfter geladen werden und dieder wird bei durchschnittlicher Nutzung täglich geladen. Wie lange macht dieser Akku das mit, bis er an Leistung verliert? Wenn der Leistingsverlust der Batterie dann fortgeschritten ist, fährt man logischerweise einen immer höheren Anteil der Strecken im Verbrennermodus. Dabei fährt man dann einfach mal so 200 km tote Batteriemasse durch die Gegend... das ist nicht sehr nachhaltig (Verbauch, Emissinen etc.). Meines Wissens kann man auch nicht nachvollziehen wie viel das Fahrzeug von seiner gesamten Laufleistung elektrisch und vieviel mit Verbrenner gefahren ist? Wer kauft sich dann solch einem Gebrauchtwagen?
Und wie siehts mit der Entsorgung eines solchen KFZ aus? Da bleibt mir nur zu sagen, dass dieses Konzept dann das Schlechteste aus beiden Antriebskonzepten vereint, sofern bis dahin kein wirklich gutes Recyclingverfahren für solche Autos entwickelt worden sein sollte.
Ich hoffe ich konnte mit dieden Zeilen etwas zum Nachdenken anregen. Denn mich regt das einfach nur auf!
184 Antworten
Zitat:
@FWebe schrieb am 10. Februar 2021 um 06:44:15 Uhr:
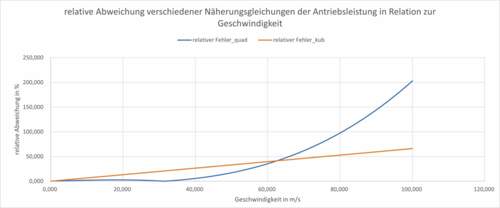
Falsch sind beide Varianten, nur weicht der quadratische im relevanten Geschwindigkeitsbereich halt weniger stark ab und ist damit definitiv die bessere Variante.
Nö. Deine Variante ist eine Näherung, ein Kochrezept, das zufällig passt. Das andere, copyright by Sir Isaac Newton, ist die physikalisch korrekte Bertrachtung. Ich wende sie nur an. Warum die korrekte Betrachtung so stark abweicht habe ich oben begründet (Stichwort vernachlässigter Reibwiderstand).
Du kannst vieles schreiben, aber bitte verbieg' nicht irgendwelche seit Jahrhunderten gültige physikalischen Gesetze.
Anbei hab' ich mal den Model S P100D durchgerechnet, mit allem PiPaPo wie Grundverbrauch (ca. 1kW), Reibwiderständen und Luftwiderstand. Da sieht das dann schon deutlich anders aus. Bis ca. 80km/h stimmt deine Näherung recht gut, da dominieren die Reibwiderstände (da entwickelt sich die Leistung quadratisch). Ab etwa 100km/h wird der Luftwiderstand dominant und es steigt mit der dritten Potenz. Was den Verbrauch angeht, so sieht man, das der Grundverbrauch (Licht, Klima/Heizung, Bordelektronik etc.) bei niedrigen Geschwindigkeiten deutlich reinhaut. Der niedrigste Verbrauch liegt irgendwo zwischen 30-40km/h, das ist auch jene Geschwindigkeit die Hypermiler mit dem Model S anvisieren.
Grüße,
Zeph
Stimmt schon, wird aber auch gerne gut gedehnt. Ich muss da gerade an einen Fall Denken eines amerik. Professors der eine nette Taylorreihe entwickelt hatte um die Flugbahn von Planeten besser zu beschreiben. Dumm nur das sich dann später erst herausgestellt hat das er den Beweis für die Korrektheit nur für das nullte Element gemacht hat.
Zitat:
@Zephyroth schrieb am 10. Feb. 2021 um 08:23:47 Uhr:
Nö.
Klar, oder wie erklärst du dir, dass deine Variante erst bei sehr hohen Geschwindigkeiten funktioniert?
Wenn du die Hälfte der Gleichung ignorierst, kannst du doch wohl kaum behaupten wollen, dass deine Werte dann trotzdem korrekt sind.
Dein Näherung ist nunmal nachweislich weiter vom richtigen Ergebnis weg als meine, da gibt es ehrlich gesagt wenig dran zu diskutieren. Damit funktioniert meine Näherung besser als deine.
Zitat:
@Zephyroth schrieb am 10. Feb. 2021 um 08:23:47 Uhr:
Das andere, copyright by Sir Isaac Newton, ist die physikalisch korrekte Bertrachtung.
Wäre sie korrekt, gäbe es keine Abweichungen, das sollte doch einleuchten, oder nicht?
Allein die Tatsache, dass du die Rollreibung ignorierst zeigt doch schon das Kernproblem auf, weshalb deine Variante auch falsch ist, ebenso wie meine.
Zitat:
@Zephyroth schrieb am 10. Feb. 2021 um 08:23:47 Uhr:
Du kannst vieles schreiben, aber bitte verbieg' nicht irgendwelche seit Jahrhunderten gültige physikalischen Gesetze.
Ich verbiege keine physikalischen Gesetze, ich ignoriere halt nur nicht die Hälfte der Gleichung, wie es bei deiner Darstellung der Fall ist, weshalb meine Variante ja auch in den genannten Grenzen deutlich besser funktioniert als deine. Die quadratische Herleitung basiert auf den korrekten Werten, während der kubische Ansatz nur die Hälfte der korrekten Werte überhaupt berücksichtigt.
Du wirst mir bestimmt das physikalische Gesetz zeigen können, welches die reine kubische Leistungsentwicklung eines Landfahrzeugs darstellt, wenn es das seit Jahrhunderten geben soll. Deine Grafik gibt dieses Gesetz zumindest schonmal nicht her.
Also nochmal:
Für relevante Geschwindigkeitsbereiche funktioniert die rein kubische Betrachtung viel zu ungenau und ist deshalb ungeeignet.
Die Faktoren, welche dies beschreiben, habe ich dir doch sogar vorgerechnet und in Bezug zum korrekten Ergebnis gesetzt.
Wenn bei einer Verdopplung der reale Faktor 5 rauskommt, die quadratische Näherung von 4 ausgeht und die kubische von 8, welche Näherung ist dann die genauere?
Deine Grafik bestätigt genau das, was ich geschrieben habe, weshalb mir der Sinn der Diskussion nicht erschließt, du hast es ja sogar grafisch vor Augen. Bei 250 km/ h braucht dein Fahrzeug das fünffache der Leistung, die es bei 125 km/ h braucht. Das ergibt einen Faktor von 5, womit der quadratische Ansatz selbst bei Vmax ein genaueres Ergebnis erzielt, als der kubische.
Man sollte dazu eventuell deine ursprüngliche Behauptung berücksichtigen, weil hier sonst nämlich der Eindruck entsteht, es würde die Physik in Frage gestellt, während es in Wahrheit nur um die Frage nach der besseren Annäherung geht.
Zitat:
@Zephyroth schrieb am 09. Feb. 2021 um 19:52:48 Uhr:
Doppelte Geschwindigkeit braucht die 8-fache Leistung. Leistung geht mit der 3. Potenz, der Verbrauch mit der 2.
Wie man deiner eigenen Grafik entnehmen kann, ist diese Aussage falsch.
Zum Vergleich nochmal mein erster Kommentar dazu:
Zitat:
@FWebe schrieb am 09. Feb. 2021 um 20:41:45 Uhr:
Als Faustformel ist Tempo_0 * x = Leistung_0 * x^2 in den meisten Fällen ausreichend genau.
Der Streckenverbrauch ergibt sich aus P/ v, womit dann auch ersichtlich wird, dass der Verbrauch um den Faktor x erhöht wird.
Wie man sieht, erhebe ich mit der Näherung keinen Anspruch auf absolute Genauigkeit.
Der Begriff "Faustformel" dürfte bekannt sein.
Bei der kubischen Näherung hingegen ist man sich sicher, dass diese der "korrekten" Gleichung entspräche und kommuniziert das auch so.
Da sehe ich allein in der Behauptung schon deutliche Differenzen.
Der Verweis auf Newton ist übrigens dezent deplatziert, ebenso wie im Folgekommentar der Bezug zum "Glauben statt Wissen".
Wenn man die korrekte Gleichung gar nicht erst verwendet, braucht man auch nicht zu behaupten, man hätte das korrekte Ergebnis.
Ihr habt die Zahlen vor Augen, es liegt also nur an euch, sie auch wahrzunehmen.
Vorschlag:
Du zeigst mir in deiner Grafik den Punkt, wo eine Verdopplung der Geschwindigkeit zur Verachtfachung der Leistung geführt hat. Mir würde alternativ auch alles über einem Faktor von 6,5 genügen.
Zitat:
@halifax schrieb am 10. Februar 2021 um 11:30:22 Uhr:
@Zephyroth: Danke für deine Geduld!Physik ist halt keine Glaubenswissenschaft!
Wo geht es denn um Glauben?
Hier stehen zwei Näherungen im Raum, von denen eine faktisch besser als die andere funktioniert, das hat mit Glauben herzlich wenig zu tun.
Vielleicht fassen wir den Diskussionsinhalt mal kurz und verständlich zusammen:
Wir streiten aktuell darum, ob 2^2 oder 2^3 näher an 5 ist.
Da ist es schon interessant, was man dafür alles an Text verfassen kann.
Ähnliche Themen
Rutsch mir doch den Buckel runter. Ich werde mich nur die nicht weiter über Physikalische Grundlagen streiten.
Wieso zeigst du mir nicht einfach mal den Nachweis deiner Behauptung?
Um physikalische Grundlagen geht es übrigens gar nicht (wobei man dabei die Frage aufwerfen kann, wieso man die Rollreibung ignoriert), sondern um die Frage, welche Näherung besser funktioniert.
Im Unterschied zu dir weis ich warum (und um wieviel) meine Rechnung ungenauer ist als deine. Ich kann es auch erklären.
Deine Näherung ist in dem Fall genauer, du weisst aber nicht warum.
Ich gehe also davon aus, dass du deine Behauptung nicht belegen möchtest?
Du könntest es dir doch ganz einfach machen:
Du nimmst deine eigene Grafik und zeigst den Punkt auf, bei dem sich die Leistung beim Verdoppeln der Geschwindigkeit verachtfacht hat und schon wäre das Thema erledigt.
Zitat:
@Zephyroth schrieb am 10. Februar 2021 um 20:10:59 Uhr:
Im Unterschied zu dir weis ich warum (und um wieviel) meine Rechnung ungenauer ist als deine. Ich kann es auch erklären.
Es sollte angemerkt werden, dass deine Aussage nicht richtig wird, nur weil dir der Fehler bekannt ist, vielmehr bedeutet es, dass du gar kein Interesse an einigermaßen vernünftigen Werten hast. Deine Aussage kannst du so definitiv nicht belegen.
Zitat:
Deine Näherung ist in dem Fall genauer, du weisst aber nicht warum.
Dass meine Näherung genauer ist als deine, versuche ich dir die ganze Zeit zu vermitteln.
Ich habe nie den Anspruch auf exakte Genauigkeit erhoben, sondern es immer als Näherung für einen bestimmten Geschwindigkeitsbereich beschrieben, was man von dir nicht behaupten kann.
Ich weiß übrigens, wieso sie genauer ist, weshalb ich mich etwas wundere, dass du glaubst es besser zu wissen. Ebenso ist mir auch die Differenz zum genauen Wert bekannt, wie ich dir anhand von Zahlen schon dargelegt habe.
Das Problem ist:
Du behauptest etwas, was du nicht belegen kannst oder willst, nämlich folgendes:
Zitat:
@Zephyroth schrieb am 9. Februar 2021 um 19:52:48 Uhr:
Doppelte Geschwindigkeit braucht die 8-fache Leistung. Leistung geht mit der 3. Potenz, der Verbrauch mit der 2.
Dass die Behauptung falsch ist, lässt sich dabei schon der Berechnung der Fahrwiderstände entnehmen, interessant ist dabei jedoch, dass du mit deiner eigenen grafischen Auswertung genau diese Behauptung für den betrachteten Bereich widerlegt hast.
Deine Aussage stimmt dann, wenn wir Körper ohne Masse und/ oder mit unendlich hohen Geschwindigkeiten betrachten, nur hat das beides nichts mit der Realität von PKW zu tun und stößt auch physikalisch an seine Grenzen.
Dies lässt den Schluss zu, dass deine Aussage ebenfalls eine Näherung darstellen sollte, weil man sonst davon ausgehen müsste, dass du die physikalischen Gesetze in Frage stellst. Dabei ist die Frage nach der Genauigkeit der Näherung absolut legitim, weil natürlich eine genauere Näherung besser ist, als eine ungenauere. Diesbezüglich lässt sich festhalten, dass deine Näherung erst bei Geschwindigkeiten besser funktioniert, welche normale PKW nie erreichen, während meine Näherung vor allem bei Geschwindigkeiten funktioniert, die PKW regelmäßig erreichen.
Ich verstehe bisher ehrlich gesagt nicht, wieso du dich an deiner Aussage so festklammerst. Du hast sie dir selbst widerlegt, stimmst mir sogar zu und trotzdem bist du nicht bereit, den Fehler einzusehen.
Dabei ist es doch ganz einfach:
Bei für PKW normalen Geschwindigkeiten liefert die von mir angeführte Faustformel ausreichend genaue Werte (wie von dir grafisch und schriftlich bestätigt). Bei deutlich höheren Geschwindigkeiten und besonders leichten Körpern funktioniert dagegen deine Näherung besser.
Rein mathematisch sollte auch klar sein, woran das liegt. Obwohl die Geschwindigkeit mit der dritten Potenz in der Gleichung auftaucht, ist die üblicherweise betrachtete Geschwindigkeit zu gering, als dass der Luftwiderstand deshalb das Ergebnis so dominiert, dass die Rollreibung vernachlässigt werden kann. Mit steigendem Luftwiderstand und/ oder sinkender Rollreibung strebt die Gleichung zu dem von dir erwähnten Verhalten, nur ist dies ein Grenzfall, der in der Realität so nie erreicht wird. Der lineare Teil ist ebenfalls ein Grenzfall, der in der Realität nicht erreicht wird, weil hierfür unendlich kleine Luftwiderstände und/ oder unendlich hohe Rollreibungswiderstände notwendig sind. Es dürfte auffallen, wieso die quadratische Näherung so gut funktioniert, sie bewegt sich nämlich zwischen den beiden Grenzfällen und weicht zu jeder Richtung entsprechend zunehmend ab, wobei die Abweichung nach oben hin deutlich besser sichtbar wird.
Der Fahrwiderstand reagiert stärker auf Änderungen des Luftwiderstandes, als auf Änderungen des Rollwiderstandes, das bedeutet aber noch lange nicht, dass der Luftwiderstand das Ergebnis immer deutlich dominiert und man deshalb pauschal den Rollwiderstand ignorieren darf.
Zum besseren Verständnis habe ich den Zusammenhang mal grafisch aufbereitet.
Die konkreten Zahlen gelten natürlich nur für das von mir berechnete Fahrzeug (m=1.500 kg cw*A=0,75 m²), die Tendenz dürfte aber klar werden.
Im betrachteten Fall ist der kubische Ansatz erst ab Geschwindigkeiten >62 m/s genauer.
Moin
62 m/s.... also ab 223 kmh. Das ist so ungefähr die Durchschnittsgeschwindigkeit von Autos möchte ich behaupten.
Also, ich habs nicht mit den Formeln, nehme mal nur die Aussage:
Zitat:
Doppelte Geschwindigkeit braucht die 8-fache Leistung. Leistung geht mit der 3. Potenz, der Verbrauch mit der 2.
Dann schaue ich auf die Graphik von Zeph, auf die erste vom 10.2.21, 8:23 Uhr.
Da braucht der Wagen bei 50 kmh ungefähr (blauer Graph) 7 kW. (Verbrauch um 12 kWh)
Bei 100 kmh müßte er nach der obigen Aussage dann ja (7*8) 56 kW Antriebsleistung (blauer Graph) brauchen und 48 kWh Verrbrauchen.
Laut der Graphik aber habe ich bei 100 kmh eine Antriebsleistung von ungefähr 18 kW, was etwas mehr als das doppelte ist (2,6 fache) und einen Verbauch 15 kWh (1,25 fache). Beides weit weg von den vorhergesagten Potenzen.
Und von 100 auf 200 kmh, vorhergesagt wurden (8 fache Leistung) also 144 kW
Abglesen aber: 100 kmh mit 18 kW Antriebsleistung mit 15 kWh Verbrauch
200 kmh mit 75 kW Antriebsleistung ( 5 facher Leistung, etwas mehr als die Hälfte des mit 8 fach vorhergesagtem) und einem Verbrauch von 36 kWh also nur etwas mehr als dem doppelten von 100 kmh, nicht dem 4 fachen, der 2. Potenz.
Zwei in der Realität erreichte Verdoppelungen der Geschwindigkeit, in keiner wurde die 8 fache Leistung der vorherigen Leistung erreicht, in keiner der 4 fache Verbrauch.
Entweder stimmt die Physik nicht (Glaub ich nicht) die Graphik nicht (das liegt an euch das zu klären) oder aber die 3. Potenz ist im gefahrenen Bereich schlicht zu viel.
Schön wäre das unbeleidigt zu klären, da das Thema schon interessant ist und mir scheint das ihr beide da sehr tief in der Thematik drinne seit, auch was die Formeln anbelangt.
Moin
Björn
Zitat:
@Friesel schrieb am 12. Feb. 2021 um 10:4:17 Uhr:
Zwei in der Realität erreichte Verdoppelungen der Geschwindigkeit, in keiner wurde die 8 fache Leistung der vorherigen Leistung erreicht, in keiner der 4 fache Verbrauch.
Wie gesagt, es sind beides auch nur Näherungen, da ist es natürlich klar, dass die Ergebnisse in den meisten Fällen abweichen werden. Man muss dabei nur schauen, mit welchem Fehler man sich zufrieden gibt.
Die Formel setzt sich aus 3 Termen zusammen:
- Grundleistung unabhängig von der Geschwindigkeit (a)
- Leistung im Rollwiderstand, geht linear mit der Geschwindigkeit (b)
- Leistung im Windwiderstand, geht mit der 3. Ordnung der Geschwindigkeit (c)
also
P(v) = a + bv + cv³
Aber es gibt weit und breit keinen Term 2. Ordnung. Die Näherung von FWebe funktioniert, weil sich Reibleistung und Windwiderstand zwischen 30-130km/h in etwa gleich aufteilen und im Schnitt, in dem Geschwindigkeitsbereich ungefähr einen quadratischen Verlauf erzeugen. Zumindest sieht es ähnlich aus.
Nur hat das nix mit Physik zu tun. Ich hab' angenommen, das die Leistung im Windwiderstand deutlich früher dominant wird, insofern hab' ich mich geirrt. Aber weder ist meine Rechnung blödsinn oder falsch, ich halte mich an die Physik. Näherungen, die ich nicht verstehe, wende ich nur ungern an, selbst wenn die physikalisch korrekte, aber unvollständige Betrachtung nicht so genau ist.
Wer sich spielen will, anbei das Excel-Sheet...
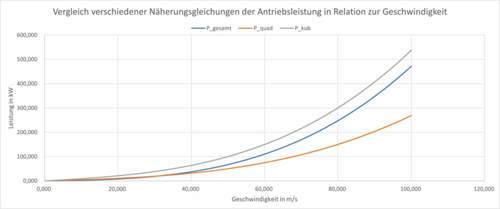
Dort sind auch beide Näherungsansätze eingezeichnet. Wie FWebe schon sagt, sein quadratischer Ansatz ist im Bereich 0-150km/h deutlich näher an der Wirklichkeit, mein reiner Ansatz nur den Luftwiderstand zu berücksichtigen ist deutlich ungenauer. Ab 150km/h nehmen sich beide Ansätze nicht viel, der quadratische zeigt zu wenig an, der 3. Ordnung um genau das zuviel.
Ein anderes Extrem ist übrigens ein F1-Auto, das fast keine Reibung (weil wenig Gewicht), aber einen lausigen cw-Wert von 1.2 hat. Hier kommt man mit dem quadratischen Ansatz überhaupt nicht zu fahren, dafür entpricht der Windwiderstand fast exakt dem Leistungsbedarf.
Grüße,
Zeph
PS.: Ich hab' die Grundleistung aus dem Excelsheet entfernt, so lässt es sich für alle Autos, egal ob Verbrenner oder E-Auto für die Antriebsleistung verwenden.
Och, jetzt hast du das Rätsel gelöst- finde ich fast ein bisschen schade.
Hat was von aufgelöstem Zaubertrick.🙄
PS: Anfangs war ja auch ständig nur die Rede vom Überwinden des Luftwiderstandes und welchen Einfluss die Geschwindigkeit hat. Egal, jetzt hat hoffentlich auch der letzte begriffen, dass sich die Physik nicht überlisten lässt. Die Rahmenbedingungen müssen ALLE berücksichtigt werden oder zumindest in erster Näherung abgeschätzt werden ob relevant (Luftdruck, Temperatur, Reifenluftdruck, ...) das verhält sich alles nicht unbedingt linear zur Geschwindigkeit, ...
Zitat:
@Zephyroth schrieb am 12. Feb. 2021 um 10:56:29 Uhr:
PS.: Ich hab' die Grundleistung aus dem Excelsheet entfernt, so lässt es sich für alle Autos, egal ob Verbrenner oder E-Auto für die Antriebsleistung verwenden.
Das habe ich ebenfalls so gehandhabt, weil es meiner Meinung nach dem diskutierten Punkt besser zuträglich ist.
Wenn man in meiner Tabelle ein wenig mit dem Gewicht und der effektiven Stirnfläche spielt, sieht man auch sehr gut, wie sich das ganze verschiebt.
Welche Näherung wann besser funktioniert, hängt konkret vom betrachteten Fahrzeug ab.
Man kann jetzt aber wohl auch besser nachvollziehen, woher meine Aussage zum "relevanten Geschwindigkeitsbereich" kommt und weshalb ich von "ausreichend genau" sprach.
Zitat:
@Friesel schrieb am 12. Februar 2021 um 10:04:17 Uhr:
(...)Dann schaue ich auf die Graphik von Zeph, auf die erste vom 10.2.21, 8:23 Uhr.
Da braucht der Wagen bei 50 kmh ungefähr (blauer Graph) 7 kW. (Verbrauch um 12 kWh)
Bei 100 kmh müßte er nach der obigen Aussage dann ja (7*8) 56 kW Antriebsleistung (blauer Graph) brauchen und 48 kWh Verrbrauchen.
Laut der Graphik aber habe ich bei 100 kmh eine Antriebsleistung von ungefähr 18 kW, was etwas mehr als das doppelte ist (2,6 fache) und einen Verbauch 15 kWh (1,25 fache). Beides weit weg von den vorhergesagten Potenzen.
(...)
Schön wäre das unbeleidigt zu klären, da das Thema schon interessant ist und mir scheint das ihr beide da sehr tief in der Thematik drinne seit, auch was die Formeln anbelangt.
Moin
Björn
Moin Björn!
Vereinfacht = auf Reibung und Luftwiderstand reduziert: P gesamt = P reibung + P luftwiderstand
Siehe
Zitat:
@Zephyroth schrieb am 12. Februar 2021 um 10:56:29 Uhr:
Die Formel setzt sich aus 3 Termen zusammen:
- Grundleistung unabhängig von der Geschwindigkeit (a)
- Leistung im Rollwiderstand, geht linear mit der Geschwindigkeit (b)
- Leistung im Windwiderstand, geht mit der 3. Ordnung der Geschwindigkeit (c)
also
P(v) = a + bv + cv³
(...)
Dazu Zahlen aus der Tabelle. 😉
Zuerst der Luftwiderstand und dessen Leistungsbedarf
50 km/h: P luft = 0,945 kW
Doppelte Geschwindigkeit = 100 km/h: P luft = 7,562 kW
"Luftwiderstand: Doppeltes Tempo = achtfacher Leistungsbedarf"
=> 7,562 /8 = 0,94525 siehe 50 km/h
Oder
100 km/h: P luft = 7,562 kW
200 km/h: P luft = 60,494 kW
=> 60,494 /8 = 7,56175 siehe 100 km/h
Dann die Reibung und deren Leistungsbedarf
50 km/h: P reib = 3,597 kW
100 km/h: P reib = 7,194 kW => 7,194 /3,597 = 2
200 km/h: P reib = 14,388 kW => 14,388 /7,194 = 2
"Reibung: Doppeltes Tempo = zweifacher Leistungsbedarf"
Beides zusammen schenke ich mir hier. 😉
Beurteilung, Interpretation, ...
Wann sind beide gleich groß? (50:50, Schnittpunkt)
Wann dominiert welche Funktion?
Wann ist dies besonders deutlich? (Je weiter man vom Schnittpunkt weg ist)
Usw.
Ich habe Zephs Tabelle und Grafik getunt.
Die Zahlen bekamen zwei Nachkommastellen mehr.
In der Grafik habe ich den Bereich verkleinert, bis 80 kW und 200 km/h, die Skalierung der Achsen verfeinert, die Kurven dicker und die Farben (s.o.) deutlicher gemacht.
Die Grafik habe ich in eine PDF-datei verbannt (s.u.), damit man die (Detail-) Ansicht richtig groß machen kann, z.B. auf 400 % stellen.
Schau dir da mal 50, 100 und 200 km/h an.
Das mit dem Verbrauch und der 2. Potenz verstehe ich auch noch nicht.
VG myinfo